本系列内容一部分素材与叙述来自于Aaron N. Siegel的Combinatorial Game Theory
组合博弈
组合博弈指的是完全信息、无随机因素的双人博弈。从简单的Nim游戏到复杂的围棋都是组合博弈。
HackenBush
HackenBush并不是最早的组合博弈游戏,但组合博弈理论中的许多想法都起源于这个游戏。
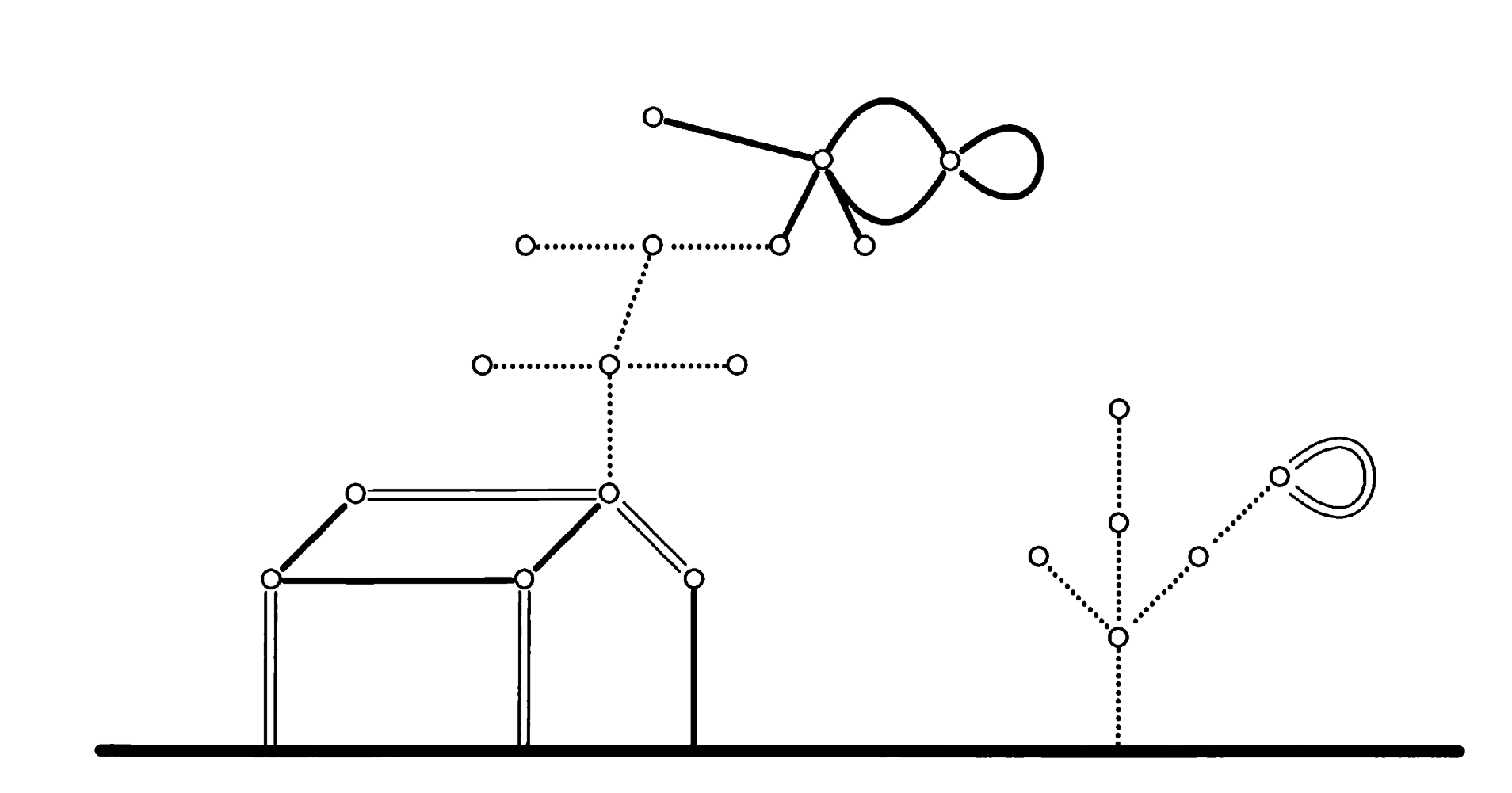
游戏的一个例子如上图,是一个染色的无向图,边有3种颜色(实边为蓝边,虚边为绿边,平行边为红边)。图的最下方有一个特殊的顶点——地面。所有的顶点与地面连通,两个玩家分别称为左玩家(左方)与右玩家(右方)。每一回合中,一个玩家可以且必须删去一条边,蓝边只能被左方删除,红边反之,绿边可以被任意玩家删除。任一条边被删去后,所有与地面不连通的顶点也一并被删去。双方交替进行游戏,当一方无法进行游戏时,另一方取胜。
注意两个玩家并不是对称的,即双方面对同样的局面,可采取的行动却不一样(左方只能删蓝绿,右方只能删红绿)。对于这一类游戏,我们称之为partizan(偏袒的),反之比如Nim就是impartial(公正的,无偏的)的。下面统一用有偏与无偏来翻译。
那么游戏进行到最后就只有下图所示的四类情况(注:对于impartial的游戏,不存在后两种情况。):

$\mathscr{N}$:先手必胜
$\mathscr{P}$:后手必胜
$\mathscr{L}$:左方必胜,无论先后手
$\mathscr{R}$:右方必胜,无论先后手
对于任何一个游戏局面$G$,采取最优策略,结果只能是四者之一,定义为$G$的结果$o(G)$
对于更为一般的局面,我们可以拆分为许多子局面。子局面的含义是:对其中任何一个的操作,都不会影响其它子局面,并且玩家每回合只能选择子局面之一进行操作。
例如在一回合中,Nim就只能对某一堆操作,HackenBush只能操作与地面相连的某一个连通分支,这种模块性是非常利于分析游戏的结构的,因此可以认为一个局面$G$与其各子局面$G_1+\cdots+G_k$是等价的,这里的加法的正式名称为析取和(disjunctive sum),以下就简称为和。
注意这里的加法运算不仅仅针对同一个游戏,不同的游戏之间的局面也可以求和,比如HackenBush的仅剩一条蓝边的局面与一个只有一堆的Nim相加,玩家每一步不得不要在两个游戏中选择其中之一操作。
选择
由于两个玩家并不对称,对于一个局面$G$,左方走一步得到的局面与右方往往不相同,为了区分这两种情况,我们称:左方走一步能到达的局面集合为$G^L$,简称为左选项(Left Option),$G^R$的定义类似。
后继局面
定义无论对于哪一个玩家,当前局面$G$走若干步能得到的局面为$G$的后继局面(subposition),这里不要求两个玩家交替走。当然这个定义也包括了$G$自身,我们用proper subposition定义排除掉$G$自身的后继局面。
play & run
从局面$G$,到其某一个后继局面的长为$k(k<\infty)$的局面序列,称为$G$的一个走法(run)
\[G_0(=G),G_1,\cdots G_k\]无限长$(k=\infty)$的走法也可以类似定义
\[G_0,G_1,G_2,\cdots\]交替走法(alternating run)指的是双方交替的走法。
一个长为$k$的交替走法称为$G$的一个play(实在不知道咋翻译😓),定义涵盖$k=\infty$或者$G_k$无法行动的情况。
等于与同构
首先不加解释的给出如下定义:对于两个局面$G,H$
\[G=H \text{ if } o(G+X) = o(H+X), \forall X.\]不难验证此处定义的等号是一个等价关系,由这个等价关系可以导出所有游戏局面的一个商集。之后会提到可以给每个商集分配一个代表元,作为这类局面的“值”。由这些“值”组成的集合定义为$\mathbb{G}$…
到这里进度可能太快了,我们还是回头看一下这个等于的性质。这里有一个简单的例子:
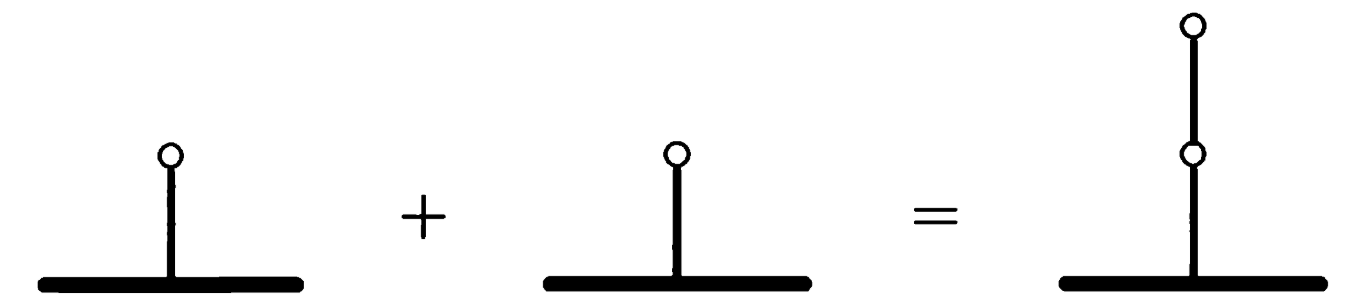
等号左边的$G_1$和右边的$G_2$都是两条蓝边,对于左方而言,无论面对$G_1+X$或者$G_2+X$,就算需要删掉这两条边,也肯定是一条一条来,不至于傻到一起删掉给自己少留一步活路。因此$G_1=G_2$。
然而,这两个情况并不完全等价,$G_1^L$只能是如下结果:
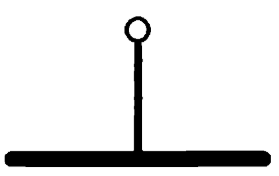
但$G_2^L$除了上面的之外,还有可能是左方犯傻一起删了,因此我们说$G_1$与$G_2$并不同构,记作$G_1\ncong G_2$
基本等式(fundamental equivalence)
回到上面,对于等号的定义。
\[G=H \text{ if } o(G+X) = o(H+X), \forall X.\]这个定义中有三个关键点的定义是值得推敲的:
- 局面的结果(outcome),$o(G)$怎么定义
- 求和(sum)方式的定义
- $\forall X$究竟是对哪些$X$
不同的定义会导致完全不同的理论,例如就第1点来说,很常见的$o(G)$的变种定义:Misère-play.
在这种规则中,无论什么游戏,走最后一步的人不会胜利,反而算作失败。这相当于调换了集合$\mathscr{N},\mathscr{P}$以及$\mathscr{L},\mathscr{R}$.虽然看起来变化不大,但自己去试一下就知道,这样的游戏策略会大不相同(当然对于无偏博弈真的只是换了一下而已)。
$X$的范围,目前语境下指的是所有的短游戏(short game)。这个概念指的是满足如下条件的$G$
- $G$的不同的后继局面数量有限
- $G$不存在无限长的走法
上面等号的定义被称之为基本等式(fundamental equivalence),在组合博弈理论中,对上式不同的定义会产生不同的理论,但是所有类似的理论又都基于这一条定义(好绕啊(lll¬ω¬))。接下来还会反复提到这个等式。

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.