前面介绍的理论中,所有局面都得画一个游戏示意图来表示,这实在是太麻烦了,作为一个数学理论,应该尽量用数字来表示。
当然,从简单的开始,先考虑只有红蓝两种颜色的双色HackenBush。关于这个简化版本的游戏,你可以从这里下载(科学上网)Windows或者Mac版本直接玩。
用整数表示局面
最简单的局面当然是一条边都没有,我们称之为空游戏(empty game),记作
\[0=\{\mid\}\]右边的记号表示$0^L=0^R=\varnothing$,即左右玩家都无法进行游戏。这样的表示法实质是用左选项和右选项来表示一个局面。这是一个很好的办法,对于只有一条蓝边的情况,就可以这么表示:

这是一个$\mathscr{L}$-局面,我们称这个局面为1,因为左方有余裕的1步选择。
进而我们可以想到,如果局面只有同种颜色的边,那么这个局面对应的数就是边的数量。只不过,对于红边而言,要再加一个负号,表示这是右方的余裕步数。
这种表示法有什么好处呢?我们看下面的局面:
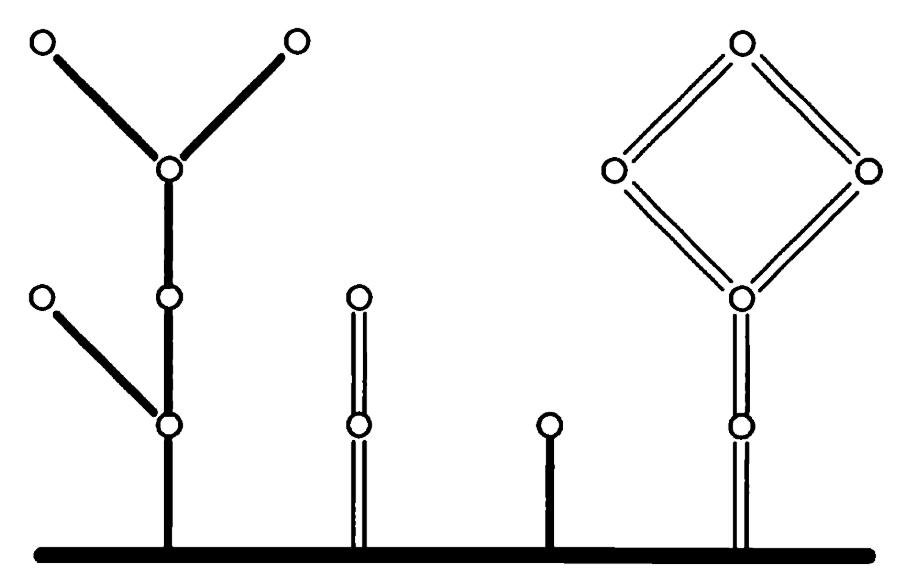
对于每一个子局面,对应的数的绝对值就是边数,只需要加起来,看看和$n$的符号,我们就知道谁输谁赢。
\[o(G)=\left\{ \begin{split} \mathscr{L} & ,\text{if }n>0\\ \mathscr{R} & ,\text{if }n<0\\ \mathscr{P} & ,\text{if }n=0 \end{split} \right.\]这里的加法,既对应于上一篇介绍的局面的disjunctive sum,也对应于一般的数的加法,可以说是很直观了。前面的图片中可以计算得到:
\[6-2+1-6=-1\]因此右方能够取胜。
下面给出几个严格的定义:
零局面
零局面指的是满足$G=0$的局面$G$,根据基本等式的定义,可以如下严格定义:
\[G=0 \text{ if } o(G+X) = o(X), \forall X.\]这样的$G$可以在求和的时候被忽略。并且很显然,每一个零局面都是$\mathscr{P}$-局面,因为$o(G)=o(0)=\mathscr{P}$.那么反之是否成立呢?
定理2.1: 如果$o(G)=\mathscr{P}$,那么$G$是一个零局面
证明:根据对称性,只需要证明如果左方能够在$X$中取胜,就也能够在$G+X$中取胜。
- 假设左方可以在$X$中后手取胜,那么右方如果在$X$中走,左方只需要按照在$X$中后手的必胜策略即可。由于$X$是短游戏,因此游戏有限步一定会结束。这样左方一定能逼迫右方在$G$中先手,左方必胜。
- 反之假设左方可以在$X$中先手取胜,假设一个获胜的后继局面是$X^L$,那么相当于在$G+X^L$中,左方有后手的必胜策略,划归到第一种情况。仍然是左方必胜。
负局面
$G$在只交换左右玩家情况下得到的局面称为$G$的负局面,记作$-G$
\[-G=\{-G^R\mid -G^L\}\]这是一个递归定义。有了这个定义,可以把$G+(-H)$简写为$G-H$。显然$o(G-G)=\mathscr{P}$,这只需要后手实施镜像策略即可。所以
\[G-G=0\tag{*}\label{s*}\]定理2.2: 如果$o(G-H)=\mathscr{P}$,那么$G=H$
证明: \(G-H=0\Rightarrow G-H+H=H \stackrel{\eqref{s*}}\Rightarrow G=H\)
有了这个定理,我们就可以通过判断两个局面的差是否是后手取胜来判断相等了。
分数?
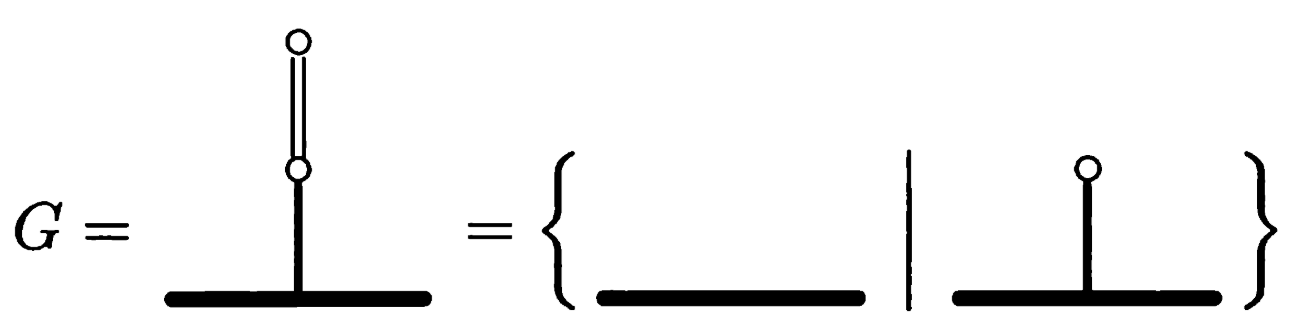
对于这个$G=\lbrace 0 \mid 1 \rbrace$,下面将证明$G+G=1$,根据定理2.2,我们只要看一看$o(G+G-1)=\mathscr{P}$是否成立。
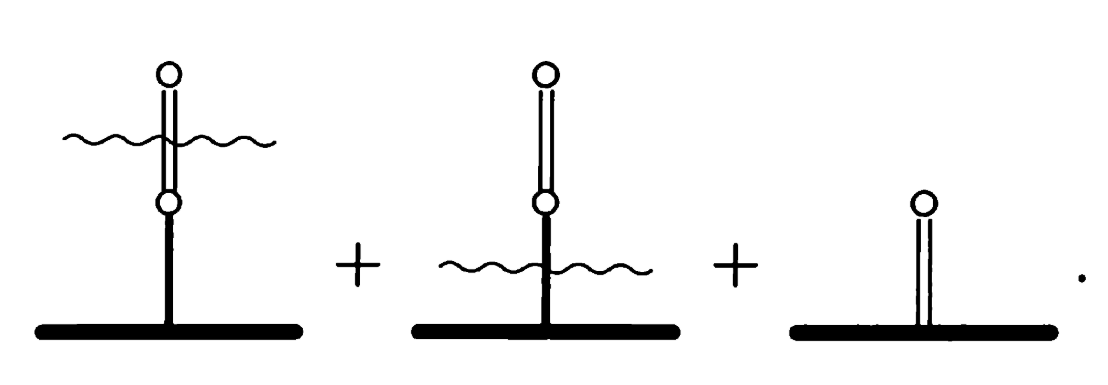
从上图中可以看出,无论先手怎么动,后手只要按照上图删边就一定能获胜(可以自己试试)。
因此可以定义$G=\lbrace 0 \mid 1 \rbrace=\frac12$
事实上可以递归证明下面的式子都成立
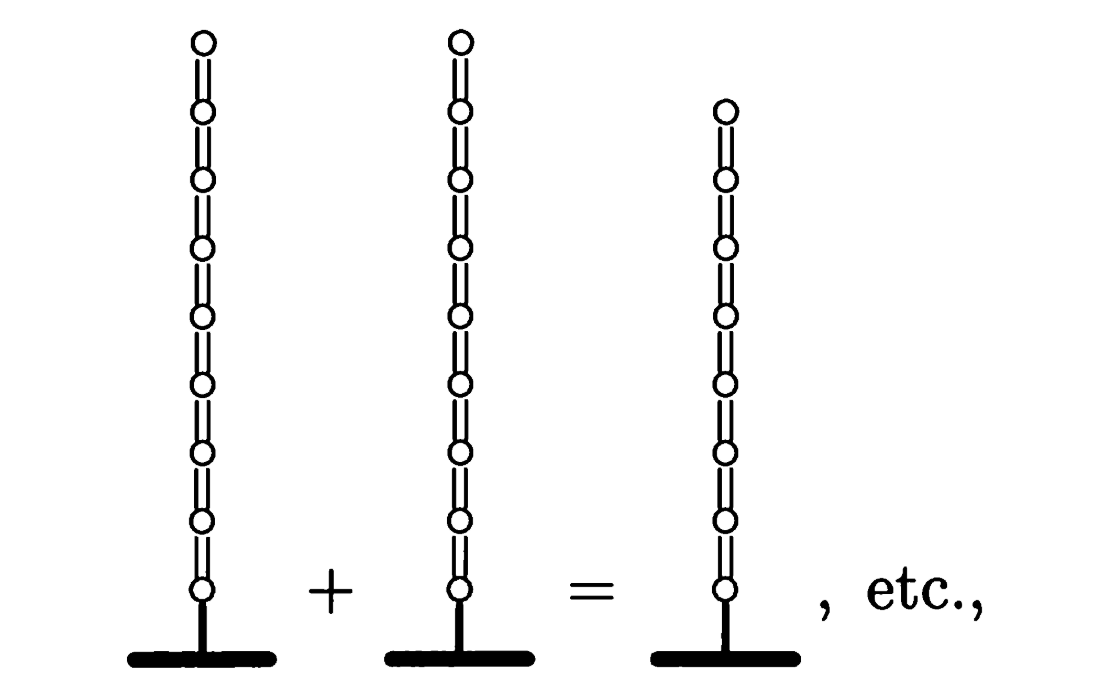
这样的话就获得了所有的形如$1/2^n$的分数。
支配(dominated)
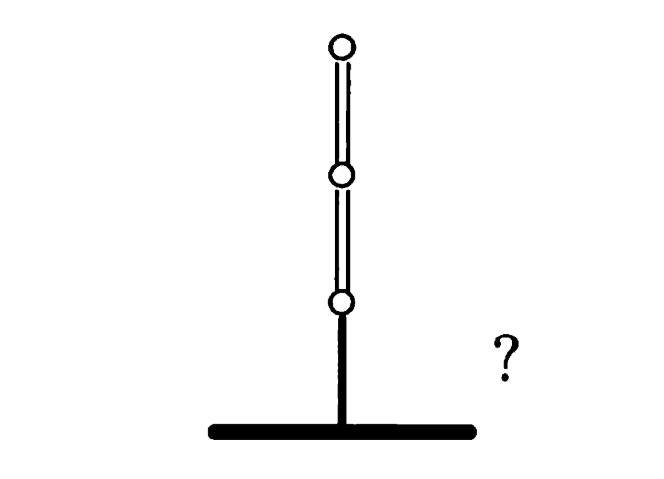
回到上面所定义的局面$G=1/4$,事实上,如果按照左右选项展开,$G=\lbrace0\mid\frac12,1\rbrace$。然而$1/2$对于右方来说是一个更好的选择,虽然在交替规则下仍然是必输。但是一旦添加一个新的局面(例如$-1/2$),那么右方就能反败为胜,而选择$1$却依然无能为力。
因此我们说右方从$1/4$到$1$的这一步被从$1/4$到$1/2$的一步所支配,通俗来说就是不如走到$1/2$好。因此我们可以写作
\[\frac14=\{0\mid \frac12\}\]可以验证$o(\frac14-\lbrace0\mid\frac12\rbrace)=\mathscr{P}$,并且进一步还可以得到
\[2^{-(n+1)}=\{0\mid 2^{-n}\}\]这是因为从$2^{-(n+1)}$到$1,2^{-1},\cdots,2^{-(n-1)}$的这些步都被从$2^{-(n+1)}$到$2^{-n}$的一步所支配
顺便我们还得到了一个小规律,那就是左方似乎会希望局面的数字尽可能的大,右方则反之。不过我们还没有定义这些局面的大小(序关系)。所以暂且放一放,之后再说。

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.