为了简便,上一篇没有讨论绿色边的情况。因此看起来似乎什么局面都能用数(注:严格来说是$\mathbb{D}$中的数,$\mathbb{D}$指二进制下的有限小数组成的环)来表示。
这一篇中我们会看到,当加入绿色边后,这套理论才会复杂起来。
首先考虑最简单的,只有一条绿边的局面$G=\lbrace0\mid0\rbrace$
看看下面的局面$G+2^{-n}$:
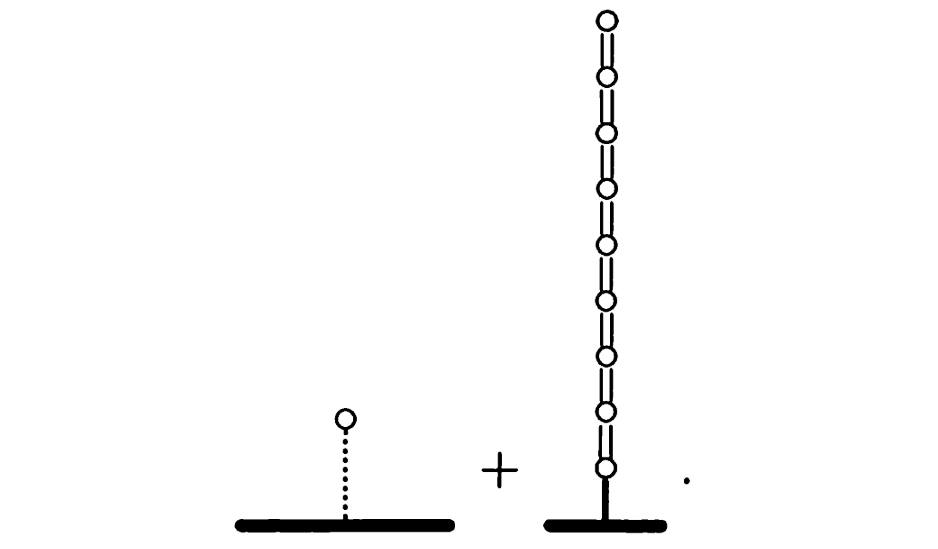
在这个局面下,无论先后手是谁,左方只要秉持:优先删绿边的策略,就能保证自己立于不败之地。反之对于$G-2^{-n}$,右方也有类似策略保证必胜。换句话说,到$G$的走法总是被支配。
根据上一篇总结的规律
\[o(G)=\left\{ \begin{split} \mathscr{L} & ,\text{if }n>0\\ \mathscr{R} & ,\text{if }n<0\\ \mathscr{P} & ,\text{if }n=0 \end{split} \right.\]似乎可以感性认识到$-2^{-n}<G<2^{-n}$,并且对于任意$n\in\mathbb{N}$成立。
然而,诡异的事情来了,根据基本等式以及$o(G)=\mathscr{N}$,因此$G\ne 0$,但是$G$似乎又比任何数字都要接近$0$.
如果你学过抽象代数,也许能够反应过来这个$G$可能根本与$0$不可比,即$G\not\gtrless 0$,但跟其它数都可以比较,这在序关系中也是常有的事。
如果还是不能理解,可以把这个“数”想象成平行于数轴上的$0$,在其它正数的左边,负数的右边,但就是跟$0$平行,不能比较。
介于这个$G$不是一般意义下的数了,需要给一个新名字,不妨叫做
\[\ast=\lbrace0\mid0\rbrace\]就此,我们打开了一个崭新世界的大门。
群$\mathbb{G}$
下面的若干定义是严格、正式的。命题除非比较难证明,否则不再赘述。
任何一个短游戏局面$G$由一个有序对$(\mathscr{G}^L,\mathscr{G}^R)$所表示,$\mathscr{G}^L$与$\mathscr{G}^R$都是比$G$更“简单”的短游戏局面组成的集合。对应的是前面所述的左选项集合,与右选项集合。可以写作
\[G=\{\mathscr{G}^{L}\mid\mathscr{G}^{R}\}\]也可以把两个集合展开,用里面的元素代替,写作
\[G=\{G_1^L,G_2^L,\cdots,G_m^L\mid G_1^R,G_2^R,\cdots,G_n^R\}\]或者更简单地写成
\[G=\{G^{L}\mid G^{R}\}\]其中$G^L$遍历集合$\mathscr{G}^L$,$G^R$遍历集合$\mathscr{G}^R$.
这是一个递归定义,递归的源头是最简单的局面$0=\lbrace\mid\rbrace$。作为一个CS专业的学生,就很容易想到这个递归过程像BFS的过程一样是可以分出层次的(第一步搜到的点,第二步等等)。
定义1.1:设$\tilde{\mathbb{G}}_0=\lbrace0\rbrace$,对于$n\ge 0$,定义 \(\tilde{\mathbb{G}}_{n+1}=\left\{ \{ \mathscr{G}^{L}\mid\mathscr{G}^{R} \} :\mathscr{G}^{L},\mathscr{G}^{R}\subset \tilde{\mathbb{G}}_{n} \right\}\)
所有的短游戏集合即为
\[\tilde{\mathbb{G}}=\bigcup_{n\ge 0}\tilde{\mathbb{G}}_n\]定义1.2:设$G,H$都是短游戏,其析取和递归定义为 \(G+H=\{G^L+H,G+H^L\mid G^R+H,G+H^R\}\tag{1}\label{s1}\)
左选项中的$G^L$遍历$G$的所有左选项,$H^L$遍历$H$的所有左选项。因而$G+H$的左选项更加严格的写法是
\[\{X+H:X\in\mathscr{G}^L\}\cup\{G+Y:Y\in\mathscr{H}^L\}\]右选项也是类似。但为了方便起见,以后会统一采用$\eqref{s1}$式的写法。
命题1.3:析取和满足交换律,结合律
定义1.4:设$G$是短游戏,$G$的负局面定义为
\[-G=\{-G^R\mid -G^L\}\]命题1.5:$-(-G)\cong G$
为了方便接下来由于递归定义,而将要遇到的大量符号表示的局面。规定两种缩写:
- 对于$G+(-H)$简写为$G-H$
- 对于$n\in\mathbb{Z},n\cdot G$表示
- 用多个竖线表示层次关系,例如
诸如此类
局面的结果 与 值
定义1.6:递归定义$\mathscr{P}^L$(指左方后手取胜的局面集合,以下类似)$\mathscr{P}^R,\mathscr{N}^L,\mathscr{N}^R$如下
\[\begin{split} \text{如果所有}G^R\in\mathscr{N}^L,\text{则}G\in\mathscr{P}^L,& \text{如果某些}G^L\in\mathscr{P}^L,\text{则}G\in\mathscr{N}^L \\ \text{如果所有}G^L\in\mathscr{N}^R,\text{则}G\in\mathscr{P}^R,& \text{如果某些}G^R\in\mathscr{P}^R,\text{则}G\in\mathscr{N}^R \end{split}\]这样就可以得到
\[\mathscr{L}=\mathscr{P}^L \cap \mathscr{N}^L,\mathscr{P}=\mathscr{P}^L \cap \mathscr{P}^R \\ \mathscr{N}=\mathscr{N}^L \cap \mathscr{N}^R,\mathscr{R}=\mathscr{P}^R \cap \mathscr{N}^R\]每一个短游戏$G$都可以通过这种方式划到某一结果里面去。记为$o(G)$。
定义1.7(基本等式):设$G,H$均为短游戏局面,那么
\[G=H \text{ if } o(G+X) = o(H+X), \text{对于任意短游戏} X.\]命题1.8:上面定义的等号是等价关系
定义1.9(局面的值):局面$G$的值定义为$G$所在的模$=$的等价类。所有值的集合定义为$\mathbb{G}$
$\mathbb{G}$上的序关系
有兴趣的话可以验证$\langle\mathbb{G},+\rangle$构成一个交换群,其关于析取和的零元为$0$,逆元由负局面给出。
下面定义序关系,首先定义结果之间的序关系。
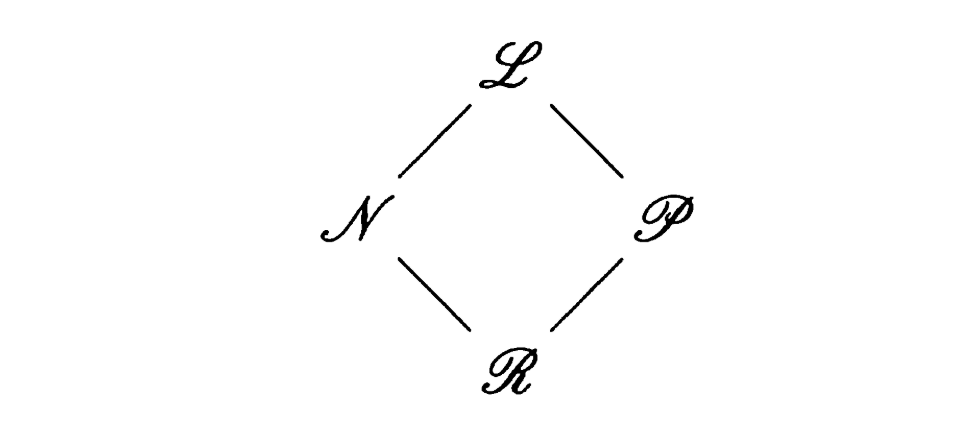
可以看出这与我们之前的想法相同,有$1>0>-1,1>\ast>-1,0\not\gtrless\ast $
定义1.10(偏序关系):设$G,H$均为短游戏局面,那么
\[G\ge H \text{ if } o(G+X) \ge o(H+X), \text{对于任意短游戏} X.\]然后需要一些额外的符号来避免总是使用$>,<$这些符号
定义1.11(其他序关系符号):设$G,H$均为短游戏局面
\[\begin{split} G\not\gtrless H(\text{or }G\parallel H) \text{ if } & G\ngeq H \text{ and } & H \ngeq G & \text{(G与H混淆(confused with))}\\ G\unicode{x29D0}H\text{ if } & G > H \text{ or } & G\not\gtrless H & \text{(G大于或者与H混淆)}\\ G\unicode{x29CF}H\text{ if } & G < H \text{ or } & G\not\gtrless H & \text{(G小于或者与H混淆)} \end{split}\]定义1.12(根据结果分类):称$G>0$称作$G$为正,$G<0$称作$G$为负,$G=0$称作$G$为零,$G\not\gtrless0$称作$G$为模糊的(fuzzy)
以上的理论已经足以让我们计算每一个游戏局面的值以及结果了。然而这只是理论上的,事实上,只要自己操作一下就会发现,计算某一个局面的值就相当于走一遍决策树。并且判断其结果的复杂度也是一样。因此以上理论目前实用性还不强,换句话说,还没有形成一种简单有效的策略。接下来的工作就是利用数学的力量探究游戏局面以及$\mathbb{G}$的性质

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.