学会使用Graphviz了,可以画彩图了2333333
兴奋的CYQ
前面我们已经认识了$0,1,-1,\ast$,这都是$\tilde{\mathbb{G}}_1$中的元素。$\tilde{\mathbb{G}}$的结构之所以复杂,很大程度就是因为$\ast$这个东西。首先我们会发现 \(\ast+\ast=0\)
这显然吗?当然,两条独立的绿边谁都可以取,那当然后手取完获胜。
因此在群$\mathbb{G}$中,$\ast$对应的等价类有$\text{ord}([\ast])=2$(这里注意一下$\mathbb{G}$与$\tilde{\mathbb{G}}$是不同的,前者是后者关于等价关系(基本等式定义)的商集,因此这里$[\ast]$指的是$\ast$的等价类)。
由$\ast$开始,衍生出来的大量局面会导致复杂的结构。
$\uparrow$局面以及衍生局面
由$\ast$组成的,有两个常见的局面,记作 \(\uparrow=\{0\mid\ast\},\downarrow=\{\ast\mid0\}\) 注意到由于$-\ast=\ast$,因此$-\uparrow=\downarrow$(回忆负号的定义)。
那么是否存在对应的真实局面呢,事实上Hackenbush游戏中不存在这个局面。因此我们需要介绍另一个游戏:青蛙与蛤蟆。
这个游戏在一个$m\times n$的棋盘上进行。棋盘的格子上有一些青蛙和蛤蟆,每回合玩家需要移动一只动物,左方只能移动青蛙,右方只能移动蛤蟆,青蛙可以向右移到一个空格内,或者跳过右边相邻格子的蛤蟆移到右边的第二个格子(也必须是空着的),右方只能移动蛤蟆,操作的方向相反。移动最后一步的玩家获胜。
说起来有点抽象,看个图就好:下面的局面就是$\uparrow=\lbrace0\mid\ast\rbrace$
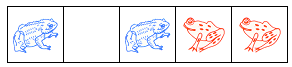
为啥呢,因为左方唯一的一步如下:
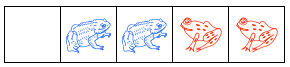
这显然是一个零局面,双方都无法继续行动。而右方的唯一一步如下:
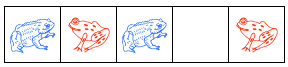
这个局面下,谁先移动,后手就被迫跳过一个动物,然后先手继续移动一步就会获胜,因此这是一个$\ast$局面。
注意到无论左方先手还是后手,这局游戏总会是左方胜,因此$\uparrow>0$
因为$1>0\Rightarrow 1<1+1<1+1+1<\cdots$能够导出所有的正整数,同样的把$1$换成$\uparrow$也成立。
有趣的是$\uparrow\not\gtrless\ast$,这是因为对于$\uparrow-\ast=\uparrow+\ast$,左方走到$\uparrow$获胜,右方走到$\ast+\ast=0$也是获胜。
那么有的小朋友就要问了,到底几个$\uparrow$能跟$\ast$相比呢?
不多不少,$2$个就够: \(\Uparrow=\uparrow+\uparrow>\ast\) 这是因为对于$\uparrow+\uparrow+\ast$,左方先手走到$\Uparrow$胜。右方先手时,只可能走到$\Uparrow,\uparrow$,都是左方胜。然而$\uparrow$这个局面太“小”,可以证明对任意正整数$n,n\cdot\uparrow<1$。
至此我们发现了,类似$\ast,\uparrow$这样的局面,总是比任何$\mathbb{D}^+$中的数小。
定义1.13:如果对于$G$的任意一个非0的后继局面(注意包括自己哦),其左右选项均不为空,则称其为dicotic(这是个生造的词)
例如$0,\ast=\lbrace0\mid0\rbrace,\uparrow=\lbrace0\mid\mid0\mid0\rbrace$都是dicotic的,然而$1=\lbrace0\mid\rbrace,1/2=\lbrace0\mid1\rbrace$就都不满足,并且容易由定义看出如果一个局面$G$不是dicotic的,那么对于任何一个$H$,如果$G$是$H$的后继局面,那么$H$也不是dicotic的。
上面这个发现说明了,具有dicotic性质的局面从某种程度上来说也是比较封闭的。事实上如果定义所有dicotic的游戏集合为$\mathbb{\tilde{G}^0}$,对应的值集合为$\mathbb{G}^0$。那么$\mathbb{\tilde{G}^0}$对于析取和封闭,并且$\mathbb{G}^0<\mathbb{G}$(子群)。
最简式
另一种常见的局面可以用Hackenbush表示
展开左右选项,得到
\[G\cong\{\ast,0\mid 0\}\]我们继续考虑$\ast+\uparrow$,根据定义,这个局面应当是 \(H\cong\{0\mid0\}+\{0\mid\ast\}\cong\{\uparrow,\ast\mid0,\uparrow\}\) 可以验证$G=H$,但是$G$跟$H$有不同的形式,并且$G$的形式更简单。因此我们希望在构造$\mathbb{G}$的时候,总是使用最简单的形式的代表元来构建。换句话说,当我们看到$H$的形式时,应该有一套有效的算法,将$H$尽快地化简为$G$甚至更简单的形式。
支配
之前其实也有提到过支配的含义,这里会严格定义。
定义1.14:设$G$是短游戏
- 如果对于某个$G^{L_1}$,存在$G^{L_2}\geq G^{L_1}$,就称之为$G^{L_1}$被$G^{L_2}$支配
- 如果对于某个$G^{R_1}$,存在$G^{R_2}\leq G^{L_1}$,就称之为$G^{R_1}$被$G^{R_2}$支配
定理1.15:设$G$是短游戏,那么如果移除$G^L$中某些被支配的局面$G^{L_1}$,得到$G’$,那么$G=G’$
证明:先证明$G’\leq G$,这只需要注意到对于$G’-G$,右方可以采取镜像策略,对$G’$与$-G$中的另一个作对称的操作即可胜利。
再证明$G’\geq G$,只需证明左方在$G’-G$中后手必胜。
事实上,只要右方不在进入走到某个$G’-G^{L_1}$,那么左方是可以采取镜像策略的。
如果右方敢走到某个$G’-G^{L_1}$,假设$G^{L_2}\geq G^{L_1}$,那么左方就可以走到$G^{L_2}-G^{L_1}\geq0$而获胜
这里的定义反映了一个现象,即左方会选取值较大的子局面,右方则反之。换句话说,最优策略中不会出现这些被支配的局面,因而在判断结果时可以忽略不计。再通俗一点说的话,就是双方不会犯傻去选择对自己差的局面。
如果你足够敏感,就可以看出这只是一个Alpha-beta剪枝操作而已。只不过由于$\not\gtrless$混淆这种关系的存在,这种剪枝不一定保证剪到只有一个最优解。
逆转
定义1.16:设$G$是短游戏
- 如果对于某个$G^{L_1}$,存在$G^{L_1R_1}\leq G$,就称之为$G^{L_1}$可通过$G^{L_1R_1}$被逆转
- 如果对于某个$G^{R_1}$,存在$G^{R_1L_1}\geq G$,就称之为$G^{R_1}$可通过$G^{R_1L_1}$被逆转
定理1.17:设$G$是短游戏,对于某个$G^{L_1}$,可通过$G^{L_1R_1}$被逆转,那么用$G^{L_1R_1L}$替换$G^{L_1}$得到
\[G'=\{G^{L_1R_1L},G^{L'}\mid G^R\}\]其中$G^{L’}$指的是$G$除了$G^{L_1}$之外的其它左选项。那么有$G’=G$。
证明:对于$G’-G$,跟前面的证明类似,后手一般都可以采用镜像策略,除非
- 左方先手走到$G^{L_1R_1L}-G$
- 右方先手走到$G’-G^{L_1}$
对于第一种情况,$G^{L_1R_1L}\unicode{x29CF}G^{L_1R_1}\leq G$,即$G^{L_1R_1L}\unicode{x29CF}G$,这个局面右方先手必胜。
对于第二种情况,左方只要走到$G’-G^{L_1R_1}$。接下来右方又有两种走法:
- $G’-G^{L_1R_1L}$,这种走法右方必败,因为左方可以使用镜像策略。
- $G^R-G^{L_1R_1}$,然而$G^R\unicode{x29D0}G\geq G^{L_1R_1} $,仍然是左方获胜。
这是一个很有意思的现象。如果一方失误走了一部臭棋,导致另一方有一种妙手,使得局面变得对失误者比下臭棋之前更差。那么就假定另一方一定会使用这一妙手(一 转 攻 势),直接用妙手之后失误者的应对得到的局面,代替臭棋。这也是逆转这个名称的来由。
定义1.18(最简式):一个短游戏$K$是最简形式当且仅当任一个$K$的后继局面都不包含被支配或可被逆转的选项。
定理1.19(存在性):对于任一个短游戏$G$,总存在$K=G$,且$K$为最简式
证明:使用归纳法,只需证明如果对于$G$的所有选项都成立可以推出$G$成立即可。
如果对于$G$的所有适当后继局面都存在最简式,那么可以用这些局面的最简式做替换。根据替换引理,替换以后$G’=G$,可以认为$G$“不变”。
如果$G$有被支配或可被逆转选项,移除掉这些选项,根据定理1.15,1.17,删除后仍然满足相等。此时的$G$已经是最简式,得证。
引理1.20:假设$G=H$,并且$G,H$都不含有被支配或可被逆转的选项,那么$\forall G^L,\exists H^L,G^L=H^L$,反之亦然,对右选项亦然。
证明:固定某个$G^L$,有$G^L\unicode{x29CF}G=H$,即等价于$G^L-H$是一个右方先手必胜局面。即对于如下局面
\[G^{LR}-H,G^L-H^L\]都是左方先手必败(右方后手必胜),即
\[G^{LR}\leq H,G^L\leq H^L\]注意前者是不可能的,这是因为会导致$G^{LR}\leq H=G$,与不含有可被逆转的选项矛盾。故只可能存在某个$H^L$使得$G^L\leq H^L$。
对这个$H^L$应用相同的方式,可以得到存在某个$G^{L’}$使得$H^L\leq G^{L’}$,但这会导致$G^L\leq H^L\leq G^{L’}$,由于$G$不存在被支配的选项,该式只能全部取等号。原命题得证。
定理1.21(最简形式定理,唯一性):假设$G=H$,且都是最简形式,那么$G\cong H$(证明应用归纳法以及引理1.20)
回到一开始的例子
\[H=\{\uparrow,\ast\mid0,\uparrow\}\]$\uparrow^R=\ast<H$(自行验证),因此左选项中$\uparrow$可通过$\ast$被逆转。$\uparrow>0$,因此右选项中$0$被$\uparrow$支配。简化之后得到
\[H=\{\ast, 0\mid 0\}\]这也是一个常见局面$H=\uparrow+\ast$,记作$\uparrow\ast$

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.
