首先指明，这里的一切优化都是针对分布式机器学习中的同步梯度下降。并且目前只考虑数据并行的分布式。

为什么需要调度GPU？

数据并行的形式化描述

数据并行的通常做法，是将数据集进行划分到各计算节点，各自训练之后求梯度，然后加和平均。一个形式化的描述如下：

设$\lbrace y_i,x_i\rbrace_{i=1}^n$是一个数据集，其中有$n$条数据，每条形如$(y_i,x_i)$，其中$x_i$表示输入，$y_i$表示预期输出。

目标函数定义为

\[F(w)=\sum_{i=1}^n\ell(x_i,y_i,w)+\Omega(w)\]

其中$\ell(x_i,y_i,w)$是一个参数为$w$的损失函数，$\Omega(w)$为正则化项。那么一个分布式的求$F(w)$最小值的算法可以描述如下：

总共$T$轮迭代，在第$t(1\leq t \leq T)$轮迭代中，共$m$个计算节点需要进行如下工作：

对训练数据集划分为$m$份，第$r$份的样本数为$n_r$。对于第$r(1\leq r \leq m)$个计算节点，读取第$r$个子训练集，$\lbrace y_{i_k},x_{i_k}\rbrace_{k=1}^{n_r}$，计算梯度：

\[g_r^{(t)}\leftarrow \sum_{k=1}^{n_r}\partial\ell(x_{i_k},y_{i_k},w_r^{(t)})\]

对$m$个计算节点获得的梯度求和（也有求平均的，对步长$\eta$的调整不同），之后做梯度下降：

\[\begin{split} g^{(t)}&\leftarrow \sum_{r=1}^m g_r^{(t)} \\ w^{(t+1)}&\leftarrow w^{(t)}-\eta(g^{(t)}+\partial\Omega(w^{(t)})) \end{split}\]

时间开销分析

数据集传输时间：数据集需要时间传输到各个节点上（无论是一开始就划分好了还是过程中传输都需要）
计算时间：计算梯度需要时间
同步时间：梯度需要加和，并且更新后的参数$w$需要广播到所有计算节点

以下的优化针对同步时间。

GPU的特点

对于单机多卡训练而言，GPU的数据传输时间很容易成为计算瓶颈。考虑到一般都会将某一个GPU映射为一个计算节点，此时同步算法就显得格外重要。

如何优化

GPU拓扑结构

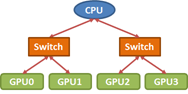
目前绝大多数Nvidia GPU服务器的GPU互联结构都是一颗PCIe二叉树，

在一台GPU服务器上执行nvidia-smi topo -m命令，可以输出GPU拓扑结构的矩阵形式。例如，一个16GPU的服务器如下：

root@compute-0-1:/# nvidia-smi topo -m
	GPU0	GPU1	GPU2	GPU3	GPU4	GPU5	GPU6	GPU7	GPU8	GPU9	GPU10	GPU11	GPU12	GPU13	GPU14	GPU15	mlx4_0	CPU Affinity
GPU0	 X 	PIX	PXB	PXB	PHB	PHB	PHB	PHB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU1	PIX	 X 	PXB	PXB	PHB	PHB	PHB	PHB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU2	PXB	PXB	 X 	PIX	PHB	PHB	PHB	PHB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU3	PXB	PXB	PIX	 X 	PHB	PHB	PHB	PHB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU4	PHB	PHB	PHB	PHB	 X 	PIX	PXB	PXB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU5	PHB	PHB	PHB	PHB	PIX	 X 	PXB	PXB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU6	PHB	PHB	PHB	PHB	PXB	PXB	 X 	PIX	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU7	PHB	PHB	PHB	PHB	PXB	PXB	PIX	 X 	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	0-11,24-35
GPU8	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	 X 	PIX	PXB	PXB	PHB	PHB	PHB	PHB	SYS	12-23,36-47
GPU9	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PIX	 X 	PXB	PXB	PHB	PHB	PHB	PHB	SYS	12-23,36-47
GPU10	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PXB	PXB	 X 	PIX	PHB	PHB	PHB	PHB	SYS	12-23,36-47
GPU11	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PXB	PXB	PIX	 X 	PHB	PHB	PHB	PHB	SYS	12-23,36-47
GPU12	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	PHB	PHB	PHB	 X 	PIX	PXB	PXB	SYS	12-23,36-47
GPU13	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	PHB	PHB	PHB	PIX	 X 	PXB	PXB	SYS	12-23,36-47
GPU14	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	PHB	PHB	PHB	PXB	PXB	 X 	PIX	SYS	12-23,36-47
GPU15	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	PHB	PHB	PHB	PHB	PXB	PXB	PIX	 X 	SYS	12-23,36-47
mlx4_0	PHB	PHB	PHB	PHB	PHB	PHB	PHB	PHB	SYS	SYS	SYS	SYS	SYS	SYS	SYS	SYS	 X 	

Legend:

  X    = Self
  SYS  = Connection traversing PCIe as well as the SMP interconnect between NUMA nodes (e.g., QPI/UPI)
  NODE = Connection traversing PCIe as well as the interconnect between PCIe Host Bridges within a NUMA node
  PHB  = Connection traversing PCIe as well as a PCIe Host Bridge (typically the CPU)
  PXB  = Connection traversing multiple PCIe switches (without traversing the PCIe Host Bridge)
  PIX  = Connection traversing a single PCIe switch
  NV#  = Connection traversing a bonded set of # NVLinks

NV#,PIX,PXB,PHB,SYS，越往后的传输速度越慢。对于没有NV#(即NVlink)的服务器，GPU的结构可以简单的建模为满二叉树。

Ring Allreduce

Ring Allreduce是高性能计算领域的经典算法，在Allreduce算法中被证明是带宽最优的。（见论文Bandwidth optimal all-reduce algorithms for clusters of workstations）。参数服务器等传统的通信结构与其相比之，在节点数量较多时，通信开销会增大。

目前主流的机器学习框架都支持NCCL后端进行通信（并声称这是Nvidia GPU上最快的通信后端）。而最新的NCCL已经将Ring Allreduce加入框架。因此，后面的优化是针对Ring Allreduce算法的。

近似优化算法

问题可以形式化的描述成：已知当前有$m$个空闲GPU，需要从当中找$n$个使得构成的环长度最短。即满二叉树$T$叶节点的最小回路$C_n$，二叉树接近树根的边权值更大。

为了简化问题，假设第$i$层的权值$d_i\gg d_{i+1}$，这当然是一个粗略的假设，实际上，只有接近上面的层数才会有这种差别。

那么下面的算法一定能够得到最小环。假设树$T$的高度为$h$

算法$f(T,m,n)$：

初始化$i\leftarrow h$
求出所有以第$i$层节点为根的子树中空闲GPU个数
如果存在某个子树中空闲节点数$\geq n$（可能有多个），转到第5步
$i\leftarrow i -1$，转到2
对于所有满足条件的子树$T’$，计算其两颗子树中空闲叶节点个数$m_L,m_R$，$\forall n_L,n_R\in\mathbb{N},n_L+n_R=m,n_L\leq m_L,n_R\leq m_R$，在两棵子树中通过$f(T_L’,m_L,n_L),f(T_R’,m_R,n_R)$找最短路（不是回路）,求出$\min_{T’}\lbrace f(T_L’,m_L,n_L)+f(T_R’,m_R,n_R)\rbrace$，得到最小路径对应的叶节点首尾依次相连即为最小环路

当然，这个算法实际对于~~更弱的条件~~$\require{enclose} \enclose{horizontalstrike}{d_i\geq d_{i+1}}$（我错了，这个条件太弱被我自己的反例推翻了），以及任意树都可以推广。

更有趣的是，该算法对于Parameter Server架构也会获得最优解。如果减弱条件为$d_i>d_{i+1}$，该算法对于Parameter Server架构仍然会获得最优解。对于Ring Allreduce，会获得一个$\frac{m}{2}-$近似解，并且最差情况可以构造出来。当然实际测试的时候基本没有出现这种极端情况。

具体证明当然只会在我的毕业论文里😜。

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.

qizhi的任务调度机制（四）

GPU调度（一）