Open Space Risk1
设$f$ 是一个可度量的识别函数,并且对于类别$y$,$f_y(x)>0$表示该对象可能属于类别$y$,$f_y(x)=0$则表示未识别。设$\cal{O}$ 为“开放空间”,并且 $S_o$ 是一个半径为 $r_o$ ,并且包含了所有已知正训练样本$x\in\mathcal{K}$和开放空间$\cal{O}$的球体。那么类别$y$的Open Space Risk $R_{\cal{O}}(f)$ 可被定义为
\[R_{\mathcal{O}}(f)=\frac{\int_{\cal{O}}f_y(x)dx}{\int_{S_o}f_y(x)dx}\tag{*}\label{risk}\]Compact Abating Probability Model2.
定义开放空间为
\[\mathcal{O}=S_o-\bigcup_{i\in N}B_r(x_i)\]其中$B_r(x_i)$是以训练样本$x_i$($N$个训练样本)为中心半径为$r$的闭球体。$r$是一个与问题相关的参数,可以根据情况调节。
首先介绍并描述Abating Bound的性质,随后将其拓展为一个为概率分布。
abating bound $A(r):\mathbb{R}\mapsto\mathbb{R}$ 是一个非负平方可积的连续递减函数。这些性质可以推出 $\lim_{r\rightarrow \infty}A(r)=0$。当$\forall x,\exists x^\ast\mid f(x)\leq A(|x-x^\ast|)$,称函数 $f$ “abating” ,因为距离 $x^\ast$越远处函数值越小。
对于核函数$K$,如果存在一个abating bound $A$ 使得
\[\forall x,x_i: 0<K(x,x_i)\leq A(\|x-x_i\|)\]那么核函数$K$abating。
为了将其推广为一个概率密度函数,我们使用训练数据定义一个随与类别$y$相关的分数$s$单调递减的的概率分布$p_f(s;y)$,其中含有RBF(径向基)核函数$K$。将这样的$p_f(s;y)$称为一个Abating Probabilistic Point Model,因为随着与训练样本的距离增加,概率密度也逐渐减小。
为了进行识别,我们将关于数据点的核函数凑成一个有效的分类模型,对于每个数据点$x_1,\dots x_m,x_i\in\mathcal{K}$得到的核函数,使用融合算子$F$,得到识别模型:
\[M(x)=p_f(F(K(x,x_1),\dots,K(x,x_m));y)\]一般来说融合算子$F$可以使用简单的求和或者求积,也可使用其他的算子。
然而,如果只使用上面的定义,$M(x)$在整个$\mathbb{R}^n$上都具有非零概率,导致$\eqref{risk}$式中在$\mathcal{O}$中积分时会产生巨大的风险值。为了避免此种情况,我们考虑对概率密度函数截断,即设定一个阈值$\tau$,得到一个新的$M_\tau$,并称之为compact abating probability Model。其具有fused abating property,即对给定的阈值$\tau$,$\forall x \in X$有
\[\min_{x\in \mathcal{K}}\|x-x_i\|>\tau \Rightarrow M_\tau(x)=0\]Open Set Risk1
给定经验风险函数$R_\mathcal{E}$, e.g. hinge loss, 开集识别的目标是找到一个可度量的识别函数,并且能够最小化Open Set Risk:
\[\mathop{\arg\min}_{f\in\mathcal{H}}\{R_\mathcal{O}(f)+\lambda_rR_\mathcal{E}(f)\}\]Open World Recognition1
Open World Recognition可用五元组$[F,\varphi,\nu,L,I]$定义,分为如下几步:
- 一个多类别的开集识别函数$F(x):\mathbb{R}^d\mapsto\mathbb{N}$,其中包含一个向量函数$\varphi(x)=\left[f_1(x),\dots,f_i(x)\right]$,该函数中对于每一个类别都有一个可度量的识别函数$f_i(x)$。并且同时用一个新类别检测器$\nu(\varphi):\mathbb{R}^i\mapsto[0,1]$,用于判断$\varphi$的结果是否属于一个未知类$(0)$。
- 标注过程$L(x):\mathbb{R}^d\mapsto\mathbb{N}^+$,对于$t$时刻的所有未知类别数据$U_t$进行标注,得到若干标注数据$D_t={(y_j,x_j)}$,其中$y_j=L(x_j)\forall x_j\in U_t$。假设在这一时刻发现了$m$个新类别,那么已知类别就变为$\mathcal{K}_{t+1}=\mathcal{K}_t\cup{i+1,\dots,i+m}$
- 增量学习函数$I_t(\varphi;D_t):\mathcal{H}^i\mapsto\mathcal{H}^{i+m}$:学习新的识别函数$f_{i+1}(x),\dots,f_{i+m}(x)$,并且加入$\varphi(x)$中。
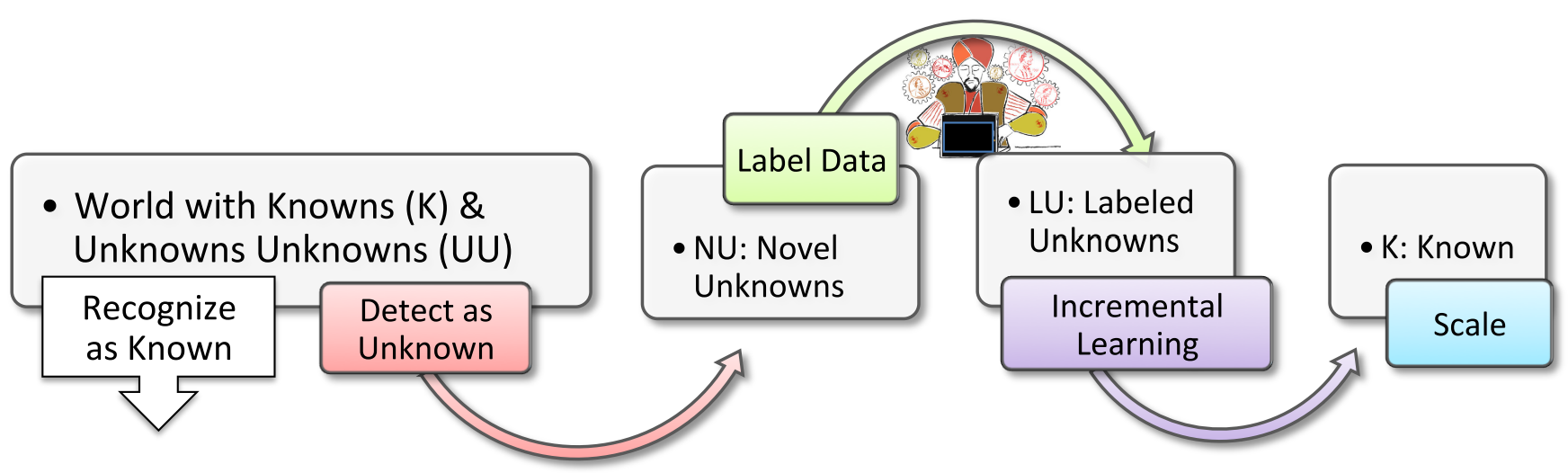
理想情况下,以上几个过程应当都是自动的,并且迭代运行。但是实际上,标注过程由人类进行。
如果我们假定$f_k(x)$表示的是样本属于第$k$类的可能性,并且对于所有类做了归一化,那么开集识别函数可以定义为
\[\begin{split} y^\ast&=\mathop{\arg\max}_{y\in\mathcal{K},f_y(x)\in\varphi(x)}f_y(x) \\ F(x)&=\left\{ \begin{array}{lcl} 0 & &\text{ if } \nu(\varphi(x))=0 \\ y^\ast & & otherwise \end{array} \right. \end{split}\]待续…
参考文献
-
Bendale, A., & Boult, T. (2015). Towards open world recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1893-1902). ↩ ↩2 ↩3
-
Scheirer, W. J., Jain, L. P., & Boult, T. E. (2014). Probability models for open set recognition. IEEE transactions on pattern analysis and machine intelligence, 36(11), 2317-2324. ↩

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.