• C2AE1
  • 闭集训练过程
  • 开集训练
    • 极值理论(EVT)
  • 开集测试
• OLTR3
  • 动态元嵌入(Dynamic Meta-Embedding)
    • 学习视觉记忆$M$
    • 构建记忆特征$v^{memory}$
    • 得到动态元嵌入
  • 调制注意力(Modulated Attention)
  • 学习过程
    • 余弦分类器
    • 损失函数
• 参考文献

C2AE¹

全文的大致思路是：根据已知类别训练一个编码器，再锁死编码器参数，根据输出重建图片。由于编码器只学习了已知类别的编码信息，预计重建结果中已知类别的重建效果会非常好，未知类别的结果会比较差，可以基于这个特点，根据重建误差的大小区分未知类别。

闭集训练过程

设定一个一个常规的交叉熵loss，假设已知类数量为$k$，输入的batch与对应的标签分别为$\lbrace X_1,X_2,\dots,X_N\rbrace\in \mathcal{K}$和$\lbrace y_1,y_2,\dots,y_N\rbrace,\forall y_i\in \lbrace 1,2\dots,k\rbrace$。

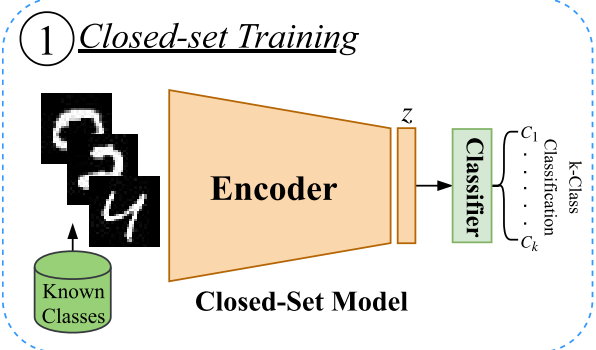
设编码器$\mathcal{F}$与分类器$\mathcal{C}$参数分别为$\Theta_f,\Theta_c$。loss定义如下：

\[\mathcal{L}(\{\Theta_f,\Theta_c\})=-\frac{1}{N}\sum_{i=1}^{N}\sum_{j=1}^{k}\mathbb{I}_{y_i}(j)\log[p_{y_i}(j)]\]

其中$\mathbb{I}_ { y_{i} }$是一个标签$y_i$的示性函数，实际上就是一个one-hot编码的向量，表征实际的类概率分布。$p_{y_{i} }=\mathcal{C}(\mathcal{F}(X_i)), p_{y_{i} }(j)$表示的是模型输出第$i$个样本属于第$j$个类别的概率。此处的交叉熵指的是是分布$\mathbb{I}_ { y_i}$与分布$p_{y_i}$的交叉熵。

公式实际上可简化，根据示性函数的定义，$y_i\neq j$时，$\mathbb{I}_{y_i}(j)=0$，因此上面的式子实际上等价于

\[\mathcal{L}(\{\Theta_f,\Theta_c\})=-\frac{1}{N}\sum_{i=1}^{N}\log[p_{y_i}(y_i)]\]

开集训练

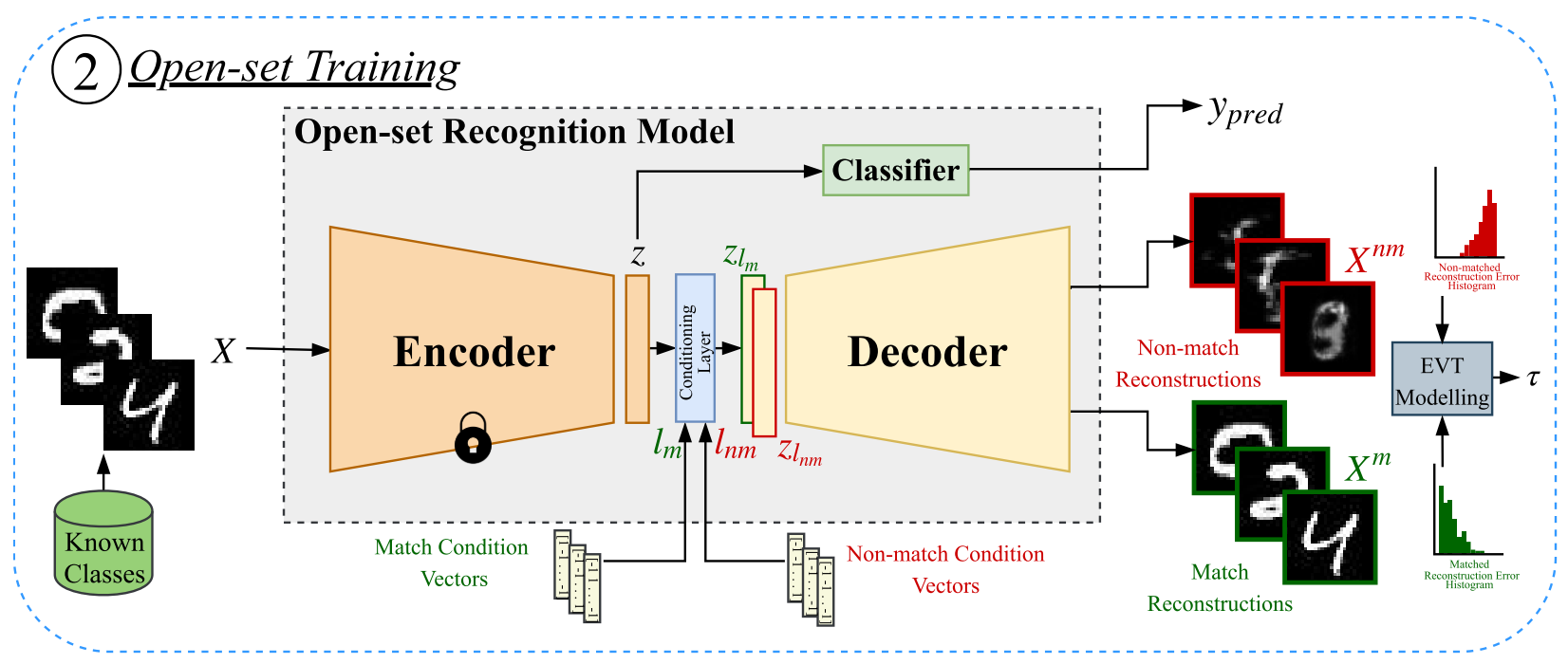
为了重建图片，首先构造一个条件层(Conditioning Layer)。我们将$\mathcal{F}$的输出特征$z$输入FiLM²模型，同时作为输入的还有标签条件向量$l_j$，定义为

\[l_j(x)=\left\{ \begin{array}{c} +1,x=j, \\ -1,x\neq j, \end{array} \right. x,j\in\{1,2,\dots,k\}\]

条件层定义如下

\[\begin{split} \gamma_j&=H_{\gamma}(l_j),\beta_j=H_{\beta}(l_j),\\ z_{l_j}&=\gamma_j \odot z +\beta_j \end{split}\]

其中$H_\gamma,H_\beta$是两个神经网络，参数分别为$\Theta_\gamma,\Theta_\beta$。输出$z_{l_j}$用于描述条件$l_j$下的隐向量$z$，即$z\mid l_j$

接下来是一个解码器$\cal{G}$（参数为$\Theta_g$），我们的期望是当标签向量$l$与实际类别相符时$(l=l_m)$，能够得到尽可能小的重建误差，此时可被视为一个传统的自编码器。如果不相符$(l=l_{nm})$，那么重建效果过应该会很糟糕。（以下用上标$m$表示类别相符(match),$nm$表示类别不相符(non-match)）

注意到对一个给定的样本$X_i$，$l_m=l_{y_{i}^{m}}$只有一个，$l_{nm}=l_ { y_i^{nm}}$却有很多（+1在其他位置）。因此在训练时我们也只随机选取一个$l_ { y_{i}^{nm}}$。设

\[\tilde{X}_{i}^{m}=\mathcal{G}(z_{l_m}),\tilde{X}_{i}^{nm}=\mathcal{G}(z_{l_{nm} })\]

分别为正确标签和错误标签时对$X_i$的重建结果，对所有样本计算以上重建结果的误差

\[\begin{split} \mathcal{L}_r^m(\{\Theta_g,\Theta_\gamma,\Theta_\beta\})&=\frac{1}{N}\sum_{i=1}^n \|X_i-\tilde{X}_i^m\|_1 \\ \mathcal{L}_r^{nm}(\{\Theta_g,\Theta_\gamma,\Theta_\beta\})&=\frac{1}{N}\sum_{i=1}^n \|X_i^{nm}-\tilde{X}_i^{nm}\|_1 \end{split}\]

其中$\lbrace X_1^{nm},X_2^{nm},\dots,X_N^{nm}\rbrace$也是取自训练集中的一组样本，并且$X_i^{nm}$与$X_i^m$属于不同的类别。

我们希望两者都尽可能小，因此损失函数定义为

\[\min_{\{\Theta_g,\Theta_\gamma,\Theta_\beta\}}\alpha\mathcal{L}_r^m(\{\Theta_g,\Theta_\gamma,\Theta_\beta\})+(1-\alpha)\mathcal{L}_r^{nm}(\{\Theta_g,\Theta_\gamma,\Theta_\beta\}),\alpha\in[0,1]\]

【疑问：第二个loss可能收敛么？

极值理论(EVT)

可以预料到，对于已知类别的图片和正确的标签向量，重建效果应当不错。但如果是全新的类别，那么无论怎样选取标签向量都不可能重建原图。那么如何设定一个阈值，使得重建误差超过该阈值就被判定为未知类比较合适呢？

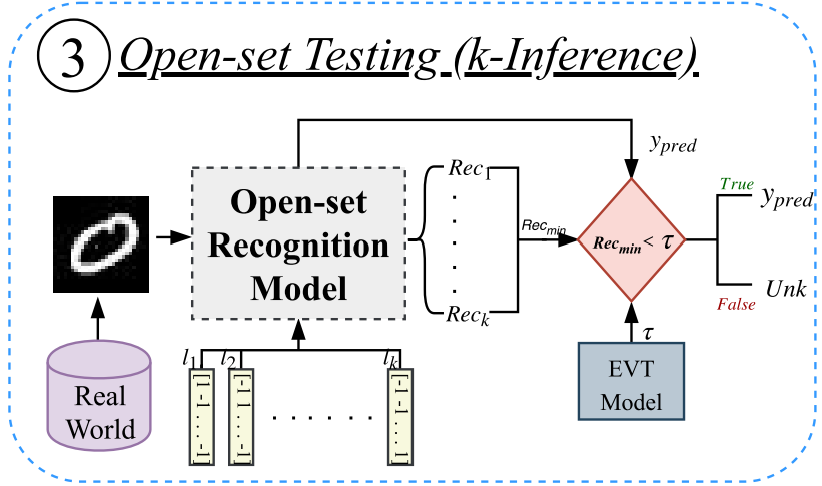
开集测试

对于输入样本$X$以及$k$个类别，将所有的$l_1,\dots,l_k$作为标签向量输入。如果$X$属于已知类，那么当中最小重建误差的那一类应该就是$X$的类别；如果$X$属于未知类，所有的重建误差都应该很大。通过EVT设定阈值，判断最小重建误差是否超过阈值，超过则为未知类，否则为已知类。

OLTR³

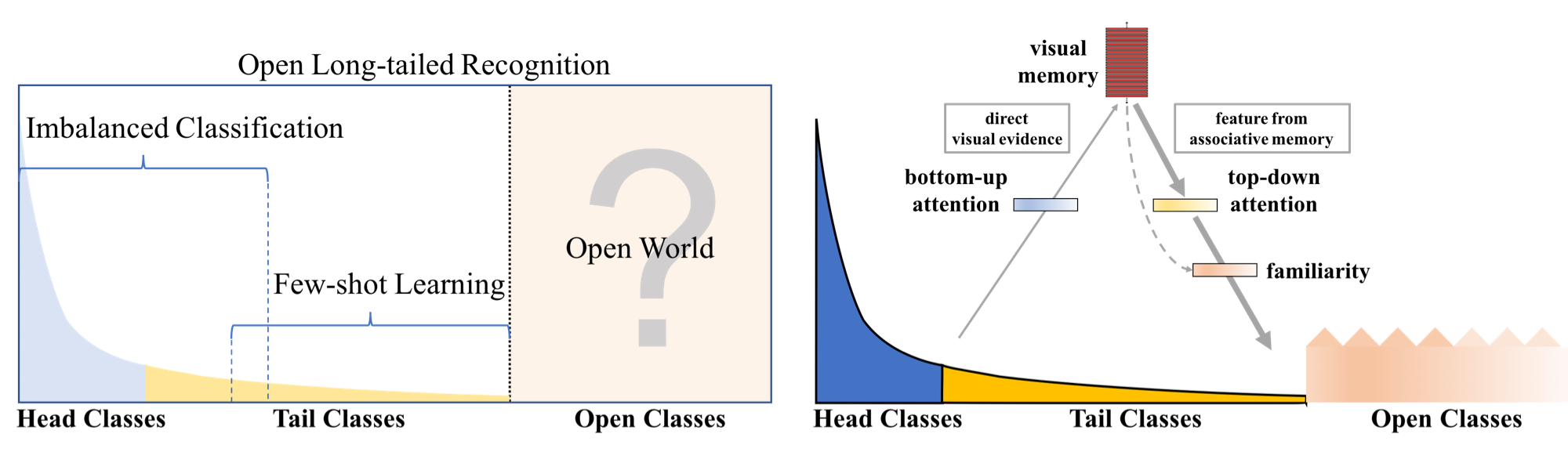
本文用一个模型同时解决三个问题：对于长尾分布的训练集，同时希望对于样本多的类别与样本少的类别进行有效的分类，同时还要将未知类正确识别。

一个显然的挑战就是，对于那些样本很少的类的某一个新样本，有很大可能被分到未知类（由于该类信息很少），反之亦然。

动态元嵌入(Dynamic Meta-Embedding)

首先用一个CNN接一个Softmax训练一个分类器，倒数第二层的输出可以看成是一个特征表示，称这个输出为直接特征$v^{direct}$。不过这个特征对于尾部类别的信息太少，不能直接使用。因此用一个记忆模块产生的记忆特征$v^{memory}$来增强$v^{direct}$。

学习视觉记忆$M$

假设训练集的类别数量为$K$，定义$M=\lbrace c_i\rbrace_{i=1}^K$。其中$c_i$是该类样本的centroid，这个centroid由两个反复交替迭代的过程得到：

1. 邻域采样(Neighborhood Sampling)：根据每一类样本的$v^{direct}$得到该类的centroid
2. Affinity Propagation：每类的centroid对于一定范围内的该类样本吸引，对其他样本排斥。得到更新后的$v^{direct}$

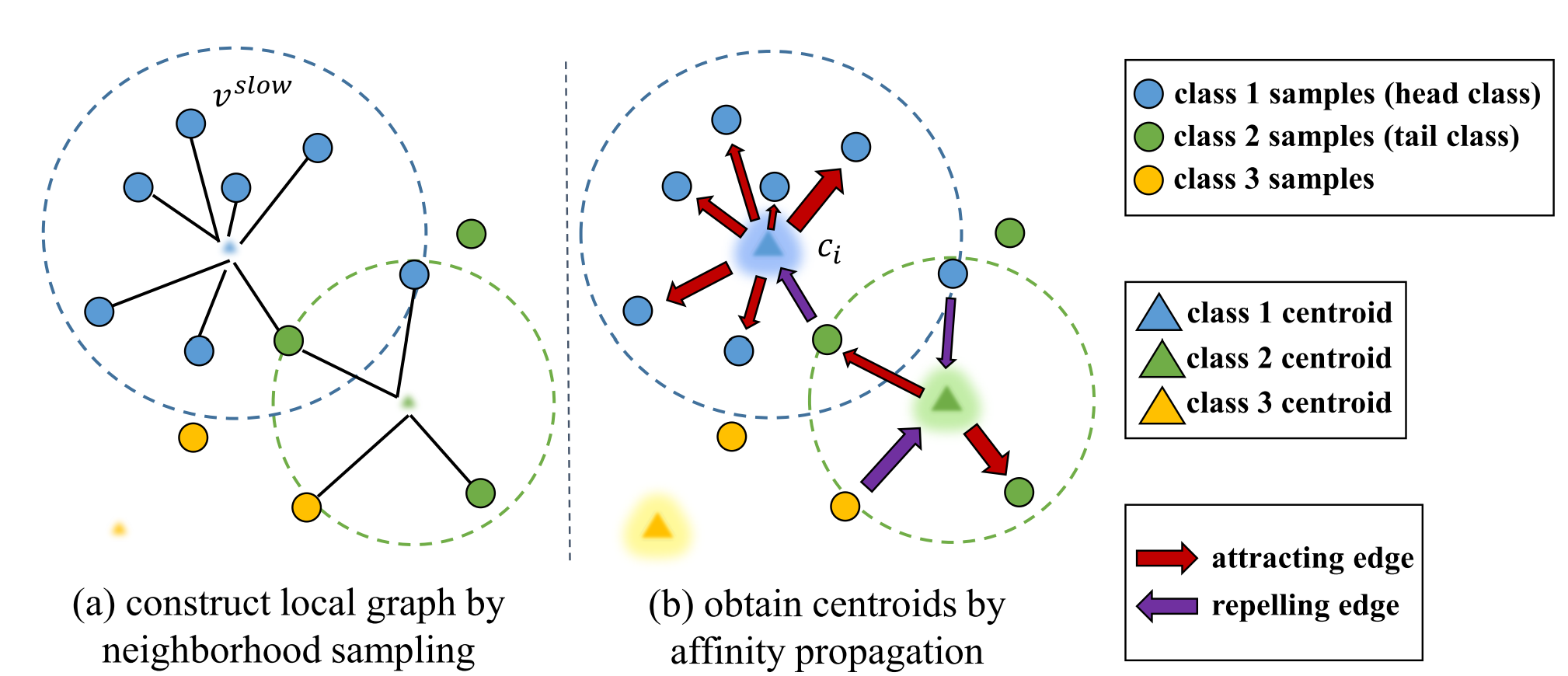
这个过程会缩小类内样本的距离，增大类间样本的距离。

构建记忆特征$v^{memory}$

记忆特征是上一步得到的所有centroid的加权

\[v^{memory}=o^TM:=\sum_{i=1}^Ko_ic_i\]

其中$o\in\mathbb{R}^K$被称为hallucinated coefficients，由一个轻量级神经网络作用于直接特征得到:$o=T_{hal}(v^{direct})$.

作者认为这一步得到的特征可以从头部类中借鉴信息，利于尾部类的分类。

得到动态元嵌入

结合直接特征与记忆特征得到$v^{meta}$

\[v^{meta}=(1/\gamma)\cdot(v^{direct}+e\otimes v^{memory})\]

其中$\otimes$为逐元素乘积

此处$\gamma$看似多余，但实际上它的定义为直接特征离最近某个类中心的距离： \(\gamma:=\text{reachability}(v^{direct},M)=\min_i\|v^{direct}-c_i\|_2\)

当样本离所有已知类中心都很远时，$\gamma$就会很大，那么既然都很远就很可能是未知类。这样取倒数之后，期望未知类的$v^{meta}$应当接近于0。这就相当于对于未知类做了特殊的编码。

对于第二个括号里的式子，作者给出的解释是：直接特征对于头部类的识别已经足够，而记忆特征加强了对于尾部类的识别。因此采用了一个soft manner权衡两者影响，即用一个轻量级神经网络作为概念选择器(Concept Selector)：

\[e=\tanh(T_{sel}(v^{direct}))\]

训练过程中对于尾部类，期望能够更多地使用记忆特征，从而自适应。

调制注意力(Modulated Attention)

作者表示：由于头部类与尾部类的判据分布在图像的不同位置(?)，因此可以添加空间层面的注意力机制，用于区分图片是属于头部类还是尾部类，并且能够提高识别效率。

调制注意力分为两部分：

1. 自注意力(self-attention):$SA(f)$
2. 条件注意力(conditional attention)（含softmax正则化）:$MA(f)$

其中$f$是CNN得到的feature map。自注意力机制来自于CVPR18的非局部神经网络⁴，文中视为一种上下文信息(contextual information)；条件注意力来自于NIPS17的Transformer结构⁵，文中视为对于自注意力的条件空间注意力（注意力的注意力）（对于自注意力各分量的选择？）。因此得到的新feature map为

\[f^{att}=f+MA(f)\otimes SA(f)\]

学习过程

余弦分类器

对于元嵌入，以及分类器$\phi$的参数$\lbrace w_i\rbrace_{i=1}^K$用如下方式进行归一化：

\[\begin{split} v_n^{meta}&=\frac{\|v_n^{meta}\|^2}{1+\|v_n^{meta}\|^2}\cdot \frac{v_n^{meta}}{\|v_n^{meta}\|},\\ w_k&=\frac{w_k}{\|w_k\|} \end{split}\]

元嵌入的归一化方法来自于Capsule Network⁶中的“squashing”函数，其作用是将短向量的长度变为接近0，长向量的长度则变为略小于1（注意第一个分式在$\Vert v_n^{meta}\Vert\rightarrow0\text{ or}+\infty$时的取值）。换言之，就是先归一化，然后根据原始的向量长度，对新向量的长度做了一个缩减。注意前面的$\gamma$对于未知类别的样本，特征向量输出会很小，因而这一做法进一步放大了缩减作用。

损失函数

整个函数可微，因而可以端到端训练。loss分为两部分：

\[L=\sum_{n=1}^{N}L_{CE}(v_n^{meta},y_n)+\lambda\cdot L_{LM}(v_n^{meta},\{ c_i\}_{i=1}^K)\]

$L_{CE}$是一个分类结果的交叉熵损失：

\[L_{CE}(v_n^{meta},y_n)=y_n\log(\phi(v_n^{meta}))+(1-y_n)\log(1-\phi(v_n^{meta}))\]

$L_{LM}$被称为large margin loss，其思想是拉近$v_n^{meta}$与其所属类中心$c_{y_n}$的距离，同时远离其它类中心：

\[L_{LM}(v_n^{meta},\{c_i\}_{i=1}^K)=\max(0,\sum_{i=y_n}\|v_n^{meta}-c_i\|-\sum_{i\neq y_n}\|v_n^{meta}-c_i\|+m)\]

文中$m$设为5.0

整个模型如下图所示

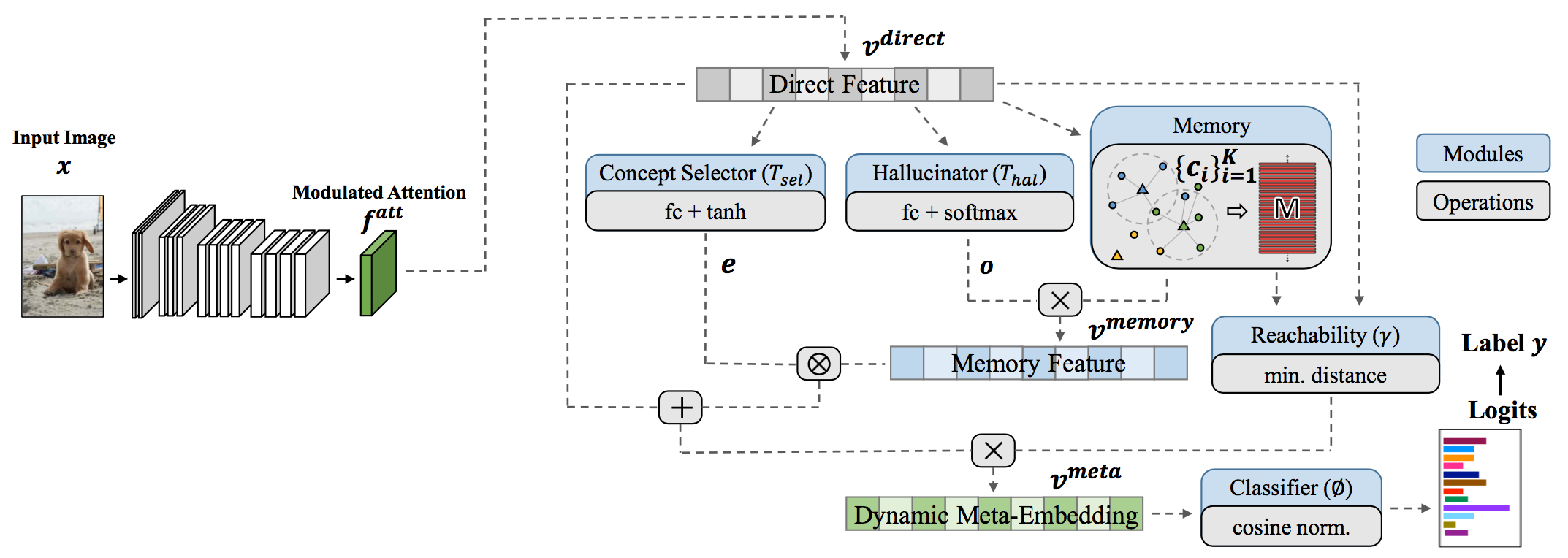
本文的同时处理不平衡训练集问题与开集识别问题，由于采用了若干策略将未知类的输出变为接近全0。因而可以在模型的其它部分通过记忆特征等办法，专注于处理不平衡训练集的问题。

参考文献

---

• Previous
  开集识别（一）
• Next
  开集识别（三）

---