• 极值理论简介
  • 极值定理(Fisher–Tippett–Gnedenko theorem)
  • 广义极值分布(GEV)
    • Gumbel分布
    • Fréchet分布
    • 逆Weibull分布
• EVM1
  • 建模
  • 简化
• 参考文献

极值理论简介

在开集识别问题中，对于输入数据提取特征之后，就要分别特征是否属于已知类。很常见的思想是选取一个阈值用于划分已知类与未知类。但是阈值应该如何选取呢？这时候就会经常用到极值理论。

极值理论跟中心极限定理类似，描述的是任意分布在样本量很大的时候的一种共同趋势。不同的是，中心极限定理描述的是整个分布，而极值理论描述的是样本中极值（最大最小值）的概率分布。

极值定理(Fisher–Tippett–Gnedenko theorem)

设$X_1,X_2,\dots,X_n,\dots$是一列独立同分布的随机变量的样本。$M_n=\max\lbrace X_1,\dots,X_n\rbrace$，如果存在实数对的序列$(a_n,b_n)$满足$a_n>0$以及

\[\lim_{n\to\infty}P\left(\frac{M_n-b_n}{a_n}\leq x\right)=F(x)\]

其中$F$是非退化的分布函数。那么极限分布$F$一定属于三种广义极值分布的一种。

这个定理的意思是，若干i.i.d分布样本的极大值分布经过线性变换后（幅度参数为正数）总能变成三种分布之一，无论原始的分布是什么。

广义极值分布(GEV)

三种GEV分别是Gumbel族, Fréchet族, Weibull族分布，分别为第Ⅰ,Ⅱ,Ⅲ类极值分布：

Gumbel分布

Gumbel分布有两个参数$\sigma,\mu\in\mathbb{R},\sigma>0$，CDF形式如下：

\[F(x;\mu,\sigma,0)=e^{-e^{(x-\mu)/\sigma} } \text{ for }x\in\mathbb{R}\\\]

Fréchet分布

Fréchet分布有三个参数$\sigma,\mu,\xi\in\mathbb{R},\xi>0$，设$\xi=\alpha^{-1},y=1+\xi(x-\mu)/\sigma$，CDF形式如下

\[F(x;\mu,\sigma,\xi)= \begin{cases} 0 & y\leq 0 \\ e^{-y^{-\alpha} } & y>0 \end{cases}\]

逆Weibull分布

逆Weibull分布有三个参数$\sigma,\mu,\xi\in\mathbb{R},\xi<0$，设$\xi=-\alpha^{-1},y=-(1+\xi(x-\mu)/\sigma)$，CDF形式如下

\[F(x;\mu,\sigma,\xi)= \begin{cases} e^{-(-y)^{\alpha} } & y<0 \\ 1 & y\geq 0 \end{cases}\]

以上分布通用的CDF形式为

\[F(x;\mu,\sigma,\xi)=\exp{\left\{-\left(1+\frac{\xi(x-\mu)}{\sigma}\right)^{-1/\xi}\right\} }\]

其中Gumbel族可视为$\xi\to 0$时的情形。

EVM¹

EVM是The Extreme Value Machine（极值机）的缩写（SVM警告）。主要思想是根据极值理论为每一个类划出一个边界，如果样本不在边界内部，就认为已经超过了该类极值的范围，从而不属于这个类。不属于任何一个类的样本就是开集样本。

官方在Github给出了本文的代码实现。

建模

设$x\in\mathcal{X}$为特征空间$\mathcal{X}$中的训练样本，$x_i$的类别标签为$y_i\in\mathcal{C}\subset\mathbb{N}$。对于距离$x_i$最近但不同类的训练样本$x_j$，定义最大边际距离为这两个样本的半距离。

对于给定的$x_i$，为了估计最大边际距离，我们可以采样若干满足$y_j\neq y_i$的$x_j$，这样就得到许多样本对$(x_i,x_j)$，每一个样本对都可以计算出一个$m_{ij}=\Vert x_i-x_j\Vert/2$。假定采样的样本为最近的$\tau$个样本对。那么这些$m_{ij}$中的最小值$\phi$就可以通过极值理论进行估计。

由于要求的是最小值，我们转而估计$z=-m_{ij}$的最大值。如果其分布非退化，由于$z<0$，因此最大值有上界0，通过相关理论专著²的结果，$z$最大值的CDF为逆Weibull分布（事实上根据PDF从右侧被截断为0可以分辨出来）。因此$\phi$的CDF为Weibull分布。

对于每一个$x_i$都可以用上述方法得到其对应$\phi$的CDF：$F_W(\Vert x’-x_i \Vert;\kappa_i,\lambda_i)$。然而我们更感兴趣的是哪些样本与$x_i$同类，因而需要使用$\phi$分布的逆$1-F_{W}(\Vert x^{\prime}-x_i \Vert ; \kappa_i,\lambda_i)$：

\[\Psi(x_i,x';\kappa_i,\lambda_i)=\exp\left\{ {-\left(\frac{\Vert x_i-x^\prime\Vert}{\lambda_i}\right)^{\kappa_i} }\right\}\]

显然这是一个随距离而递减的概率密度函数(Probability of Sample Inclusion)，这样我们对于每一个样本都可以划出一个范围，超过一定范围（概率密度太小）就认为不是同类了。

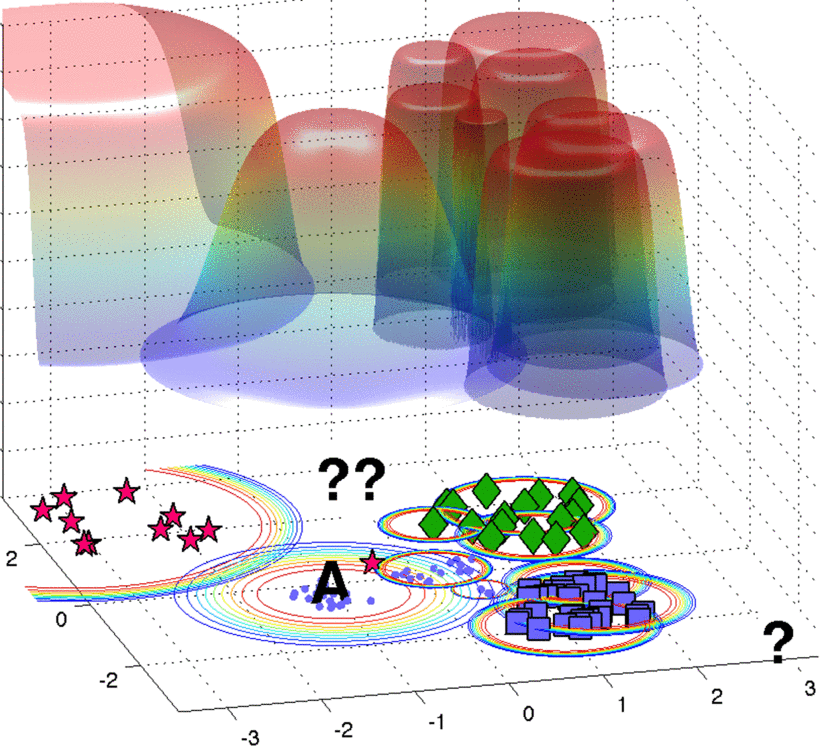
形式化的表述如下：对于样本$x’$与类别${\mathcal C}_l$，$x’$属于类${\mathcal C}_l$的概率为$\hat{P}({\mathcal C}_l \vert x^{\prime}) = \max _{\lbrace i: y_i = {\mathcal C}_l\rbrace} {\Psi\ (x_i,x^{\prime}; \kappa _i, \lambda _i)}$，即对于该类中各样本概率的最大值。我们需要在分布上选取一个阈值$\delta$，只有当某个新样本$x’$对其他样本的概率都小于$\delta$时，才认为不属于任何一个类，即为未知类，这样就解决了开集识别问题。

\[y^* = \begin{cases} \arg \max_{l \in \lbrace 1,...,M\rbrace} \hat{P}({\mathcal C}_l\vert x^\prime) & \text{if } \hat{P}({\mathcal C}_l\vert x^\prime) \geq \delta \\ { \text{"unknown"} } & \hbox {Otherwise.} \end{cases}\]

简化

这个模型理论上很完备，但是几乎不可能使用。想一想，对每个样本都有一个$\Psi$需要维护，搞得像径向基(RBF)网络³一样，理论上十分优秀，但数据量一大就废了，可能么？

实际上，同一类$\mathcal{C}_l$的$N_l$个样本中，很多样本的概率密度函数$\langle x_i,\Psi (x_i,x^{\prime},\kappa _i,\lambda _i) \rangle$是有重叠的，在样本空间中某个位置，只要有一个概率密度超过$\delta$，就已经可以判别可能属于该类了，更不要说同类其他样本的叠加。

因此，有许多$x_i$是冗余的，只需要选择所有样本的一个子集，就能达到相同的判别效果。现在问题就变成至少要选几个。

作者在这里先给出了一个判别是否为冗余的方法：设定另一个阈值$\varsigma$，对于某个类，一个一个的添加样本，假设新添加的某个样本$x_j$离该类已有的某个样本$x_i$太近了，即

\[\Psi _i(x_i,x_j,\kappa _i,\lambda _i) \geq \varsigma\]

那么就认为$\langle x_j,\Psi_j (x_j,x^{\prime},\kappa _j, \lambda _j) \rangle$是冗余的。

经过这样的逐步选择过程，最终的模型里有一些样本的概率密度函数留了下来，就称这些留下来的样本为极端向量。设其示性函数$I(\cdot)$为：

\[I(x_i)= \begin{cases} 1 & \text{if } \langle x_i,\Psi (x_i,x^{\prime},\kappa _i,\lambda _i) \rangle \text{ kept}\\ 0 & \text{otherwise}. \end{cases}\]

那么简化问题就变成以下目标函数的优化：

\[\text{minimize } \sum _{i=1}^{N_l} I(x_i) \text{ subject to}\\ \forall j \exists i \mid I(x_i) \Psi (x_i,x_j,\kappa _i,\lambda _i) \geq \varsigma\]

然而这本质上是一个集合覆盖问题，即NP-完全问题。对于这个组合问题的研究很多，作者使用了贪心策略，根据以往对这个问题的结果⁴，可以获得$(1+\ln (N_l))$的近似解，并且在任何多项式时间的近似算法中误差上界最小，为$(1-o(1))\cdot \ln(N_l)$。

参考文献

---

• Previous
  开集识别（二）
• Next
  运维日常踩坑——Docker

---