话说搞AI还要懂实分析么……这么多数学工具怎么学的过来……
Domain Gap
Domain Gap 是迁移学习中一个客观存在的影响因素,主要表现在两个数据集(域)上的差异。一般认为Domain Gap 越大,迁移的难度也越大。但是目前的 Domain Gap 的计算往往使用一些不同的方式,比如MMD(maximum mean discrepancy)1,最优传输理论中的 Wasserstein 距离2等等。
是否存在一个客观的指标能够描述域之间的迁移难度呢?2018年的一篇文章3对此进行了分析。
域的刻画
首先我们要形式化刻画数据集,即域。我们将一个域看成两部分:数据生成过程与标签过程。这两个过程都可以看作是各自域上的一个概率分布,即在空间的某个位置生成数据的概率密度有多大,以及在这个位置的数据被标为不同类的概率有多大。
数据生成过程
设源域与目标域分别为$\mathcal{X}^s,\mathcal{X}^t$。源域上的数据生成分布为$p^s(\bm{x})$(对应概率测度$\mathbb{P}^s$),目标域上的的记号类似。以下假设$T_{ts}:\mathcal{X}^t\to\mathcal{X}^s$是一个双射,其逆为$T_{st}:=T_{ts}^{-1}$。
标签过程
源域的标签过程的真实分布设为$p^s(y\mid\bm{x})$,对于目标域的标签过程的分布,类似假设真实的分布是$p^t(y\mid\bm{x})$。
迁移
实际上我们学习的标签过程会是一个连续概率分布,而不是$p^s,p^t$那样的离散版本。对于源域学习的标签过程我们可以看作是假设空间$\mathcal{H}^s:=\lbrace h^s:\mathcal{X}^s\to\mathbb{R}\rbrace$中的一个元素(也就是一个函数)。
对于目标域学习的标签过程我们就不这么定义了,而是看成将目标域的数据先通过$T_{ts}$作用之后迁移到源域进行识别,其假设空间为:
\[\mathcal{H}^t:=\{h^t:\mathcal{X}^t\to\mathbb{R}\mid h^t(\cdot)=h^s(T_{ts}(\cdot))\text{ for some }h^s\in\mathcal{H}^s\}\]也就是说,$\mathcal{H}^t$是依赖于$\mathcal{H}^s$与$T_{ts}$的。
这里就涉及到核心问题了:$T_{ts}$该怎么选?
接下来有一点测度论内容了,但可以通俗理解
对于可测映射$T_{ts}:\mathcal{X}^t\to\mathcal{X}^s$,概率测度$\mathbb{P}^t$,我们可以定义一个pushforward distribution,这个概率分布的定义域为在源域上,可以看作经过$T_{ts}$从定义在目标域的$\mathbb{P}^t$传输到源域的一个概率分布,记为 \(\mathbb{P}^{\#}:=(T_{ts})_{\#}\mathbb{P}^t\)。
根据Wikipedia上面的描述,这个东西其实就是\(\mathbb{P}^\#:=\mathbb{P}^t\circ T_{ts}^{-1}=\mathbb{P}^t\circ T_{st}\)。设\(p^\#(\bm{x})\)为其概率密度,那么\(\mathbb{P}^\#\)也类似的定义了一个域的数据生成,我们称这个域为传输域(transport domain)。
我们定义传输域上标签过程的分布为\(p^\#(y\mid\bm{x})=p^{t}(y\mid\bm{x}^t)\),这里$\bm{x}^t=T_{st}(\bm{x})$。也就是说,我们把源域的数据通过$T_{st}$传到目标域,无论这个映射是否靠谱,都按照目标域的真实标签分布分类。
一般期望损失
假设函数$\ell(\cdot,\cdot)$为预测标签与真实标签之间差异的某种损失函数,那么对于域之间的迁移,我们定义如下期望损失:
\[R^{a,b}(h):=\int\ell(y,h(\bm{x}))p^b(y\mid\bm{x})p^a(\bm{x})dyd\bm{x}\]其中$a,b$均属于集合\(\lbrace s,t,\#\rbrace\),$h$属于$\mathcal{H}^s$或$\mathcal{H}^t$。并且对于$R^{a,a}$简记为$R^a$。
我们试图估计如下式子的界:
\[\Delta R(h^s,h^t):=\left\vert R^t(h^t)-R^s(h^s)\right\vert\]相信很多人被前面的这一通操作搞得莫名其妙,我来解释一下。
首先来看$R^s(h^s)$这一项,展开就是
\[R^{s}(h^s):=\int\ell(y,h^s(\bm{x}))p^s(y\mid\bm{x})p^s(\bm{x})dyd\bm{x}\]它的含义是:按照源域生成分布生成的数据$\bm{x}$,在源域被标记为某个$y$,所造成的与$h^s$标签结果的差异$\ell(\cdot,\cdot)$的期望。这里面跟数据集(域)本身无关的有
- 损失函数$\ell(\cdot,\cdot)$的选择
- 假设空间中$h^s$的确定
再来看$R^t(h^t)$,展开为
\[R^{t}(h^t):=\int\ell(y,h^t(\bm{x}))p^t(y\mid\bm{x})p^t(\bm{x})dyd\bm{x}\]由于$h^t(\cdot)=h^s(T_{ts}(\cdot))$,上式变为
\[R^{t}(h^t)=\int\ell(y,h^s(T_{ts}(\bm{x})))p^t(y\mid\bm{x})p^t(\bm{x})dyd\bm{x}\]含义是:按照目标域生成分布生成的数据$\bm{x}$,在目标域被标记为某个$y$,与被传输到源域之后用$h^s$标签结果差异$\ell(\cdot,\cdot)$的期望(也就是迁移学习的过程)。这里面跟数据集(域)本身无关的有
- 损失函数$\ell(\cdot,\cdot)$的选择
- 假设空间中$h^s$的确定
- 传输函数$T_{ts}$的选取
可以说$R^{t}(h^t)$描述了迁移的难度,这个难度一方面体现在:源域本身通过选取$h^s$的分类就是有损失的。另一方面,传输函数也会很大程度影响迁移的效果。
如果我们确定了$\ell(\cdot,\cdot)$,那么我们就可以通过精心选择$h^s$与$T_{ts}$来最小化$R^{t}(h^t)$。但这是困难的,我们退一步去找$\Delta R(h^s,h^t)$的界。
界
以下结果的推导详情请看论文3。
假设问题仅仅是二分类(可推广到多分类),两类标签分别是$+1,-1$。并且满足损失函数$\ell(\cdot,\cdot)$有界:
\[\sup_{h^s\in\mathcal{H}^s,x\in\mathcal{X}^s,y\in\{1,-1\}}\left\vert\ell(y,h^s(\bm{x})\right\vert:=M<\infty\]那么如下不等式成立
\[\Delta R(h^s,h^t)\leq M\left(\mathcal{W}_{c_{0/1}}(\mathbb{P}^s,\mathbb{P}^\#)+\min\{\mathbb{E}_{\mathbb{P}^\#}[\Vert\Delta p(y\mid\bm{x})\Vert_1],\mathbb{E}_{\mathbb{P}^s}[\Vert\Delta p(y\mid\bm{x})\Vert_1]\}\right)\]其中,\(\Delta p(y\mid\bm{x}):=p^t(y\mid T_{st}(\bm{x}))-p^s(y\mid \bm{x})\)。而 \(\mathcal{W}_{c_{0/1}}(\cdot,\cdot)\)为关于联合分布\(c_{0/1}(\bm{x},\bm{x}')=\bm{1}_{\bm{x}\neq\bm{x}'}\)的Wasserstein 距离。\(\bm{1}_{\bm{x}\neq\bm{x}'}\)的含义是仅在\(\bm{x}\neq\bm{x}'\)时返回1,否则返回0。
去掉绝对值之后,移项很容易得到
\[R^{t}(h^t)\leq R^{s}(h^s)+M\left(\mathcal{W}_{c_{0/1}}(\mathbb{P}^s,\mathbb{P}^\#)+\min\{\mathbb{E}_{\mathbb{P}^\#}[\Vert\Delta p(y\mid\bm{x})\Vert_1],\mathbb{E}_{\mathbb{P}^s}[\Vert\Delta p(y\mid\bm{x})\Vert_1]\}\right)\label{target}\tag{*}\]为了方便理解,首先简单介绍Wasserstein距离。
Wasserstein 距离
Wasserstein 距离(以下简称W距离),是衡量两个概率分布距离的一种方式
\[\mathcal{W}(\mathbb{P},\mathbb{Q})=\inf_{\gamma\in \Pi(\mathbb{P},\mathbb{Q})} \iint \gamma(\bm{x},\bm{y}) d(\bm{x},\bm{y}) d\bm{x}d\bm{y}\]对于两个概率分布$\mathbb{P},\mathbb{Q}$,W距离希望找到一个最好的联合分布$\gamma$,使得$(\bm{x},\bm{y})$服从分布$\gamma$时,其距离$d(\bm{x},\bm{y})$的期望最小。
文中的距离为形如$[c(\bm{x},\bm{y})^p]^{1/p}$的形式,其中$p>0,c$为某个代价函数,$\eqref{target}$中为0/1的代价函数。
在$\eqref{target}$的右侧各项中,$R^s(h^s)$只与源域上的分类器效果相关。含$\Delta p(y\mid\bm{x})$的项由于涉及到目标域上的真实标签分布$p^t$而无法计算,优化也无从谈起。因此作者选择仅对W距离这一项进行优化。
对这一项的优化又可写作
\[\min_H=\mathcal{W}_{c,p}(H_\#\mathbb{P}^t,\mathbb{P}^s)\]$H$对应之前的$T_{ts}$。
作者将$H$拆分为两个映射$H(\bm{x})=H^2(H^1(\bm{x}))$。$H^1$为从目标域$\mathcal{X}^t$映射到联合空间$\mathcal{Z}$的单射,$H^2$则从联合空间映射到源域$\mathcal{X}^s$,就变成了学习
\[\min_{H^1,H^2}=\mathcal{W}_{c,p}\left((H^2\circ H^1)_\#\mathbb{P}^t,\mathbb{P}^s\right)\]将W距离也展开,得到
\[\min_{H^1,H^2}\min_{G^1:H^1_\#\mathbb{P}^t=G_\#^1\mathbb{P}^s}\mathbb{E}_{\bm{x}\sim \mathbb{P}^s}\left[c\left(\bm{x},H^2\left(G^1(\bm{x})\right)\right)^p\right]^{1/p}\label{target2}\tag{**}\]$G^1$是从源域$\mathcal{X}^s$到联合空间$\mathcal{Z}$的单射。
$\eqref{target2}$就应该是作者的优化目标函数了,然而\(H^1_\#\mathbb{P}^t=G_\#^1\mathbb{P}^s\)这个约束很难直接从优化的角度刻画,因此直接被做成了一个正则项。
\[\min_{H^1,H^2,G^1}\left(\mathbb{E}_{\bm{x}\sim \mathbb{P}^s}\left[c\left(\bm{x},H^2\left(G^1(\bm{x})\right)\right)^p\right]^{1/p}+\alpha D(G_\#^1\mathbb{P}^s,H^1_\#\mathbb{P}^t)\right)\]$D(\cdot,\cdot)$是用于衡量两个概率分布距离的某种度量方式。当$\alpha\to +\infty$时,上式的目标就与$\eqref{target2}$等价。
作者加入了另一个对称的重建项,得到最后算法实际的优化目标
\[\min_{H^{1:2},G^{1:2}}\left({\color{red}{\mathbb{E}_{\bm{x}\sim \mathbb{P}^s}\left[c\left(\bm{x},H^2\left(G^1(\bm{x})\right)\right)^p\right]^{1/p}+\mathbb{E}_{\bm{x}\sim \mathbb{P}^t}\left[c\left(\bm{x},G^2\left(H^1(\bm{x})\right)\right)^p\right]^{1/p}}}+{\color{blue}{\alpha D(G_\#^1\mathbb{P}^s,H^1_\#\mathbb{P}^t)}}\right)\label{wtarget}\tag{#}\]这个式子的几何含义如下图所示
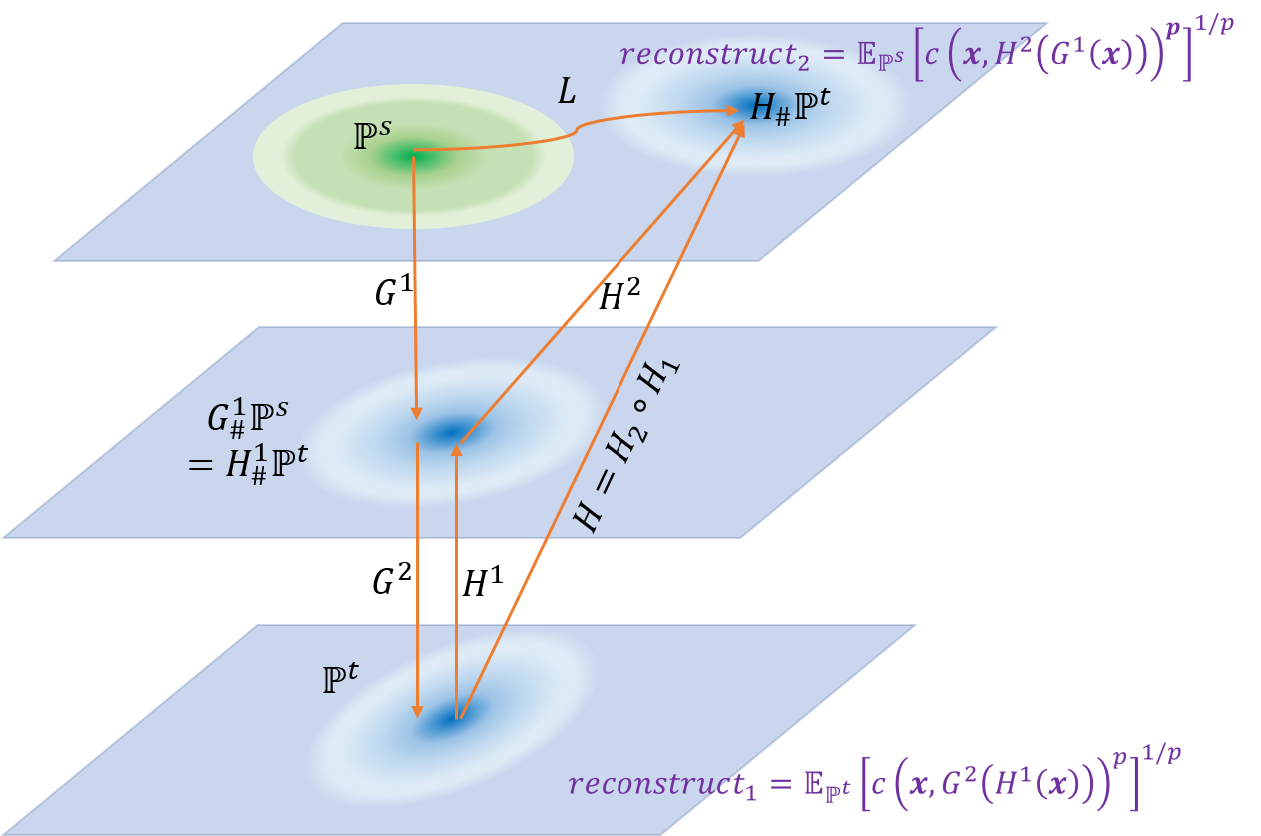
算法实际学习了从源域到目标域的映射$G=G^2\circ G^1$和从目标域到源域的映射$H=H^2\circ H^1$,并且希望满足约束的同时尽可能减小两个重建误差项。
网络设计
采用了类似GAN的思想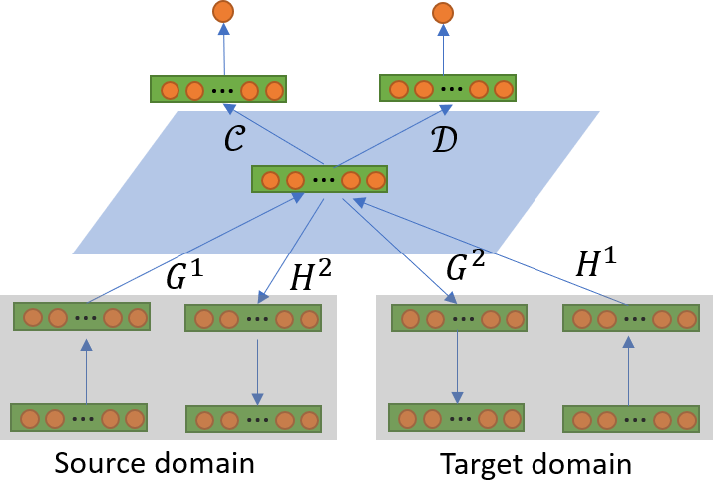
在使用$\eqref{wtarget}$的优化目标的同时,训练一个分类器$\mathcal{C}$与判别器$\mathcal{D}$。分类器用于在联合域$\mathcal{Z}$上对映射过来的样本进行分类。判别器$\mathcal{D}$用于判别联合域上的样本是属于源域还是目标域。当无法区分时,认为两个域在联合域上的分布已经足够接近。
待训练的参数有$G^{1:2},H^{1:2},\mathcal{C},\mathcal{D}$。其中
\[\begin{split} (G^{1:2},H^{1:2},\mathcal{C})&=\mathop{\arg\min}_{G^{1:2},H^{1:2},\mathcal{C}}\mathcal{I}(G^{1:2},H^{1:2},\mathcal{C})\\ \mathcal{D}&=\mathop{\arg\max}_{\mathcal{D}}\mathcal{J}(\mathcal{D}) \end{split}\]这里的$\mathcal{I}$是$\eqref{wtarget}$的loss加上分类器$\mathcal{C}$的分类loss,再减去判别器的交叉熵loss;$\mathcal{J}$是判别器$\mathcal{D}$的loss。
\[\begin{split} \mathcal{I}(G^{1:2},H^{1:2},\mathcal{C})&=\color{red}\mathbb{E}_{x\sim\mathbb{P}^t}[c_\gamma(\bm{x},G^2(H^1(\bm{x})))] +\mathbb{E}_{x\sim\mathbb{P}^s}[c_\gamma(\bm{x},H^2(G^1(\bm{x})))]\\ &+\color{green}{\mathbb{E}_{(\bm{x},y)\sim\mathcal{D}^s}[\ell(y,\mathcal{C}(G^1(\bm{x})))]}\\ &+\color{blue}{\alpha[\mathbb{E}_{\bm{x}\sim\mathbb{P}^s}[\log(\mathcal{D}(G(\bm{x})))]+\mathbb{E}_{\bm{x}\sim\mathbb{P}^t}[\log(1-\mathcal{D}(G(\bm{x})))]]} \end{split}\]实验时,选取了\(c_\gamma(\bm{x},\bm{x}')=2/[1+\exp\{-\gamma\Vert\bm{x}-\bm{x}'\Vert_2\}]-1,\gamma=100\),是由非常“尖”的高斯分布产生的,可以近似0/1代价函数。
小结
本文作为一篇理论的文章形式化并比较深入的分析了Domain Gap,并且尝试进行了优化。然而问题非常多:
- 从目标域映射到源域是正常的设定,但能否映射到其它域呢?文中的优化过程提到了联合域,不清楚时优化过程中自然出现的还是强行加上去的。
- 对$\eqref{target}$优化只是在优化Gap的上界,而不是Gap本身,这可能是最后性能较差(见论文中)的一个原因。
- 选取W距离进行优化的原因是因为其他项没关系?且不说源域分类损失那一项,后面那一项即使不知道目标域的真实标签分布$p^t$,就不能用伪标签么?省掉的这一项对于性能的影响,作者只用了一个人工数据集实验,完全没有说服力。
- 同时学习$G^1,H^1,G^2,H^2$四个映射和GAN,我觉得很有难度,没有代码很难说服我。
参考文献
-
Gretton, A., Borgwardt, K., Rasch, M., Schölkopf, B., & Smola, A. J. (2007). A kernel method for the two-sample-problem. In Advances in neural information processing systems (pp. 513-520). ↩
-
Courty, N., Flamary, R., Tuia, D., & Rakotomamonjy, A. (2016). Optimal transport for domain adaptation. IEEE transactions on pattern analysis and machine intelligence, 39(9), 1853-1865. ↩
-
Le, T., Nguyen, K., Ho, N., Bui, H., & Phung, D.Q. (2018). On Deep Domain Adaptation: Some Theoretical Understandings. ↩ ↩2

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.