神经图灵机(NTM)是Google DeepMind 的工作1,主要思想是将图灵机中存在的一些离散过程转化为可微分的连续过程,通过神经网络模拟图灵机的工作过程。本质上仍然是RNN的变体。
结构
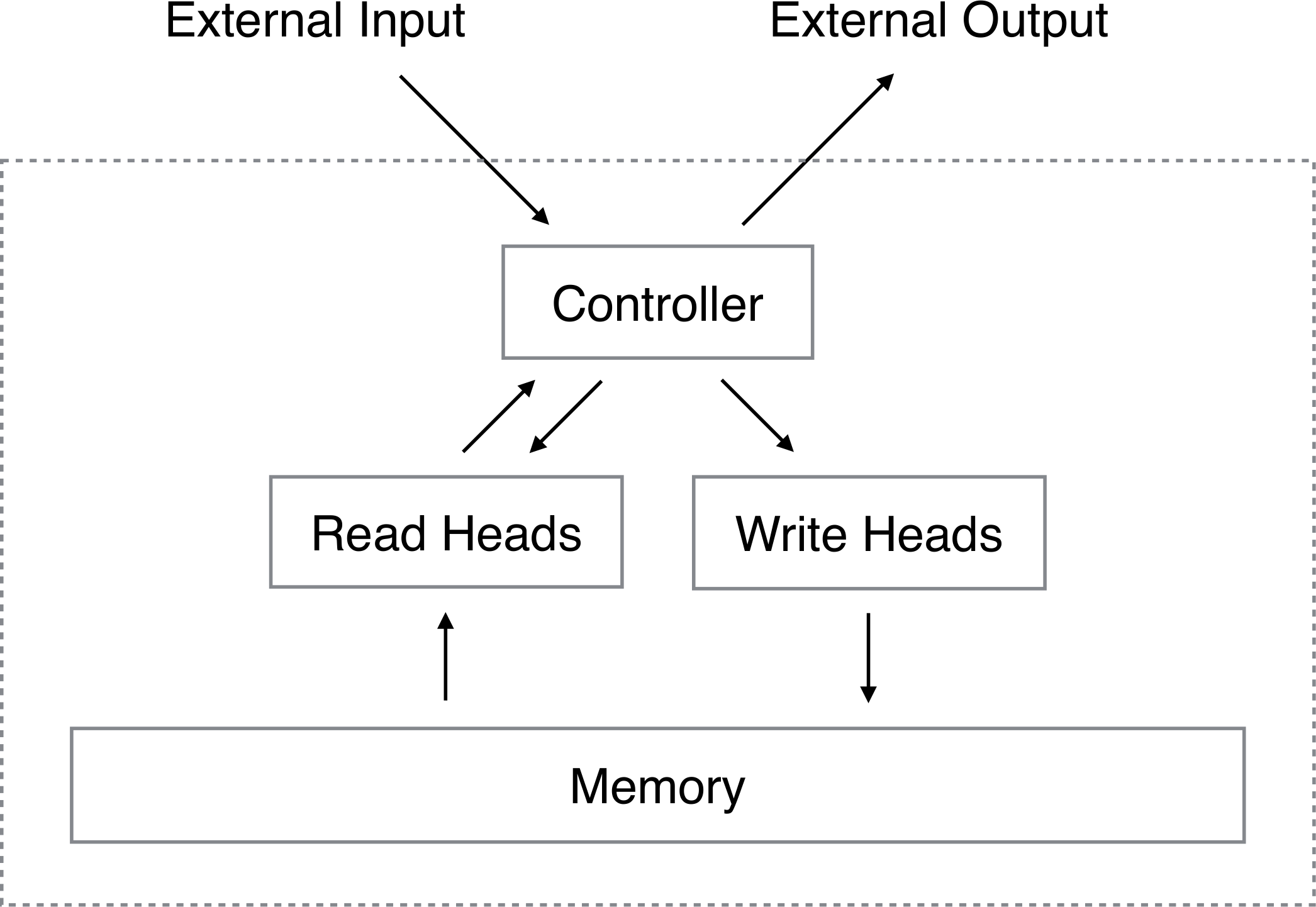
由于模仿的是图灵机,因此NTM有着与图灵机基本类似的架构,主要部件有:一个由神经网络模拟的控制器,一个存储。
控制器的行为同时取决于输入以及存储中读取的信息,通过输出与外界交互的同时也向存储中写入数据。一个图灵机的功能基本上靠的是对控制器设计一个合适的有限状态机(FSM)实现的,这也是NTM中需要采用神经网络模拟的原因之一。
工作原理
由于有读写两个不同的过程需要控制,因此需要分别设计。

读
记\(t\)时刻的存储为\(\bm{M}_t\),该存储是一个\(N\times M\)的矩阵。其中\(N\)是矩阵中条目的数量,每个条目是一个长为\(M\)的向量。
读磁头对应的网络应当输出一个长为\(N\)的权重向量\(\bm{w}_t\),该向量是归一化的。
\[\sum_i w_t(i)=1,\qquad 0\leq w_t(i)\leq 1,\forall i.\]读磁头读取到的内容是一个长为$M$的向量\(\bm{r}_t\),跟存储中一个条目的大小相同。我们知道,图灵机往往只离散的读取某一个位置的条目,而为了使得这一过程可微分,NTM读取到的信息设计为所有$N$个位置条目的加权和,即:
\[\bm{r}_t\longleftarrow\sum_i w_t(i)\bm{M}_t(i)\]换言之,每次读磁头的读取都利用了整个内存的信息。权重只是使得读取的选择性变得连续。
写
作者此处受LSTM中输入门与遗忘门的启发,将写过程分为两个阶段:擦除(erase)和加(add)。
擦除
擦除过程指的是将存储中的每个条目按某个系数缩减,不同位置的条目缩减的系数不同,这个系数由写磁头得到的一个权重向量\(\bm{w}_t\),和擦除向量\(\bm{e}_t\)共同决定。
\[\tilde{\bm{M}}_t(i)\longleftarrow \bm{M}_{t-1}(i)\otimes[\bm{1}-w_t(i)\bm{e}_t]\]\(\bm{1}\)是一个全1的行向量,\(\otimes\)指的是逐元素相乘。擦除向量长为\(M\),其元素均位于\([0,1]\)。
注意到只有当擦除向量为全1,并且权重向量对应位也为1时,这个向量才会被真正擦除为0。另外,这两者只要有一个为0,那么就不会发生擦除。
由于按元素乘运算\(\otimes\)满足交换律,因此多个并行擦除操作的顺序对最终结果没有影响。
加
如果说前面的擦除只是类似LSTM的遗忘门,那么这里才是真正的写入新数据。
写磁头会生成一个加数向量\(\bm{a}_t\),按权重\(w_t\)加在对应的结果上:
\[\bm{M}_t(i)\longleftarrow \tilde{\bm{M}}_t(i)+w_t(i)\bm{a}_t\]跟按元素乘法一样,这里的加法也满足交换律,因而加的顺序不会造成影响。并且这两个操作都是可微的。
这里的一乘一加两个操作共用了权重\(\bm{w}_t\),我简单地将其分量理解为:有多大的意愿修改存储中的这个条目。当其权重的在某个存储位置的分量较大时,将会尽可能用新的内容取代该位置上旧的存储内容。
寻址机制
事实上,读写头的权重向量\(\bm{w}_t\)是同一个控制器生成的。那么这个权重该如何产生呢?这就涉及到NTM的寻址机制。
NTM的寻址并不是固定某一个内存位置,而是通过设置\(\bm{w}_t\)各分量的大小,设置一次读写对不同位置的关注程度。作者将这个寻址过程描述为两步:
基于内容寻址
每个读写头会输出一个长为\(M\)的key vector $\bm{k}_t$,然后将其与存储矩阵的每一个条目\(\bm{M}_t(i)\)计算相似度\(K[\cdot,\cdot]\)。根据相似度的大小做变换后归一化得到初步的权重(寻址偏好):
\[w^c_t(i)\longleftarrow\frac{\exp(\beta_tK[\bm{k}_t,\bm{M}_t(i)])}{\sum_j\exp(\beta_tK[\bm{k}_t,\bm{M}_t(j)])}\]这里将相似度按参数key strength \(\beta_t\)等比例放大后进行softmax,得到一个不同内存位置的概率分布。
key strength用于控制这一步寻址的聚焦程度,\(\beta_t\)越大权重就越集中。相似度采用的是余弦相似度。
\[K[\bm{u},\bm{v}]=\frac{\bm{u}\cdot\bm{v}}{\|\bm{u\|\cdot\|}\bm{v\|}}\]基于位置寻址
只使用基于内容寻址有一个明显的问题,就是对于任务的不同类型输入泛化性不会很好。假如训练了一个用于计算\(f(x,y)=x\times y\)的NTM,那么我们期望的是NTM总能从存储中的两个固定位置取出数据并且相乘,而与这两个位置具体存的内容完全没有关系。
插值门
为了控制前一步中基于内容寻址的影响大小,引入插值门参数\(g_t\in(0,1)\)
\[\bm{w}^g_t\longleftarrow g_t\bm{w}_t^c+(1-g_t)\bm{w}_{t-1}\]该参数将控制接下来的权重有多大程度来自于基于内容寻址或者上一时刻的权重。
移位权重
图灵机的读写头是需要移动的,假设\(g_t\)总是很小,NTM的读写头也不能一直保持不动,因此需要一个方式描述究竟读写头要移动几位。
这里的设计是将读写头的移动看成是连续的,生成一个移位向量 \(\bm{s}_t\),假设需要移动6.7位,就设\(s_t(6)=0.3,s_t(7)=0.7\),其余位为0。移位具体的计算方式是用一个循环卷积实现。
\[\tilde{w}_t(i)\longleftarrow\sum_{j=0}^{N-1}w_t^g(j)s_t(i-j)\]其中\(i-j\)的计算\(\mod N\)进行。
循环卷积存在的一个显著问题是:由于循环卷积核可被视为一个模糊算子,经过若干时刻后各个内存位置的权重会越来越接近。因此采用幂函数锐化(sharpen)这些权重(注意用的不是softmax的指数函数)
\[w_t(i) \longleftarrow \frac{\tilde{w}_t(i)^{\gamma_t}}{\sum_j \tilde{w}_t(j)^{\gamma_t}}\]其中\(\gamma_t\geq 1\).
总的来说,这套寻址机制在设计时考虑了三种不同的寻址情况
- 完全基于内容相似度的寻址。
- 基于内容相似度,但访问位置移动。使得可以在若干次访存中访问一个连续的数据块。
- 完全基于位置的寻址。使得可以以某个固定的步长访问一块内存区域。
完整的寻址流程如下图所示:
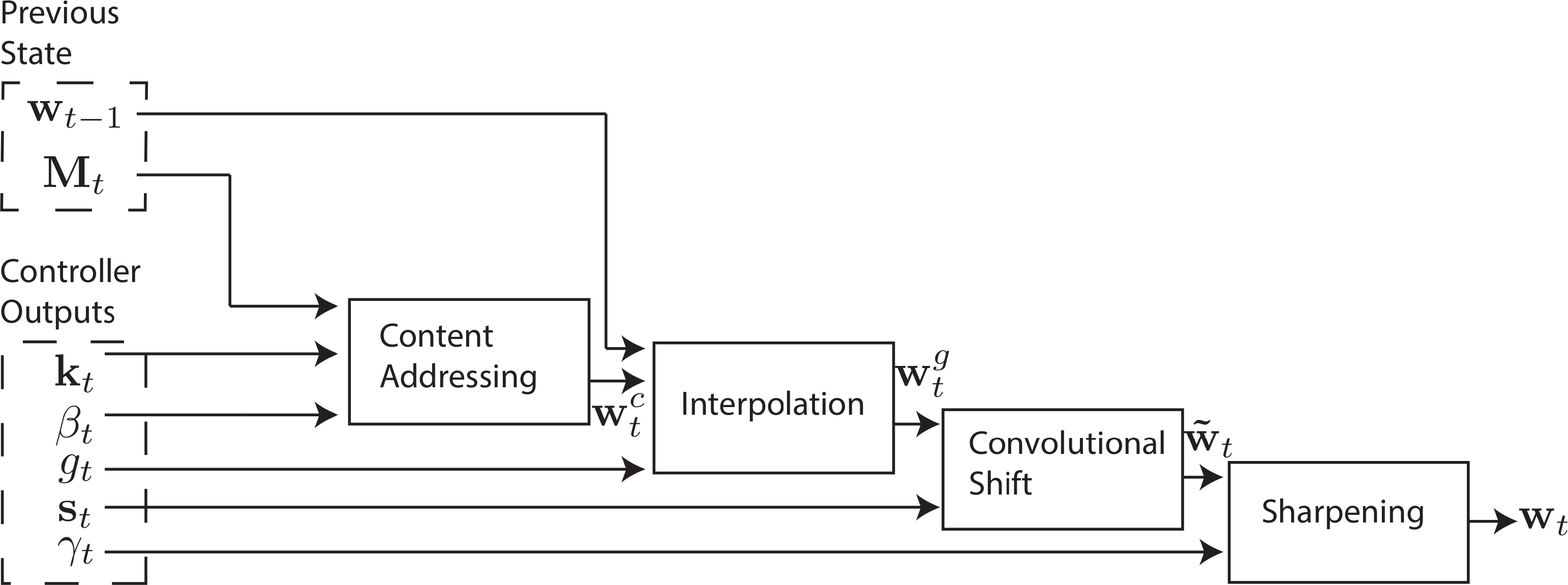
控制器网络设计
很坑的是,这篇文章并没有直接给出具体的网络设计。作者简单提了一下可以使用一般的前馈网络或者某种RNN,两种方法的优劣如下:
- 前馈网络
- 由于没有RNN的内部状态,可解释性更强
- 可以通过反复读写一个位置模拟RNN,但效率很低
- RNN
- 自带存储(内部状态),类比CPU的寄存器
大量对这篇文章的复现都产生了一些问题,如训练时梯度变为NaN,或者极慢的收敛速度。直到2018年的一个开源Tensorflow复现2,被ICANN接收,并作为Tensorflow的官方实现NTMCell。
完整的架构如下图所示

实验
一个自然的验证想法是:对于一些功能简单的程序,将其输入和输出作为训练数据喂到NTM中,看NTM是否能够模拟出这些程序的运行。
复制
复制任务指的是当用户输入若干个等长向量(8bit)组成的序列(包含间隔符)时,NTM应当输出一个内容完全相同的序列。这个任务可以检测NTM是否能够存储并且“回忆”起某个内容与长度都任意的向量。
首先作者对性能进行了测试:
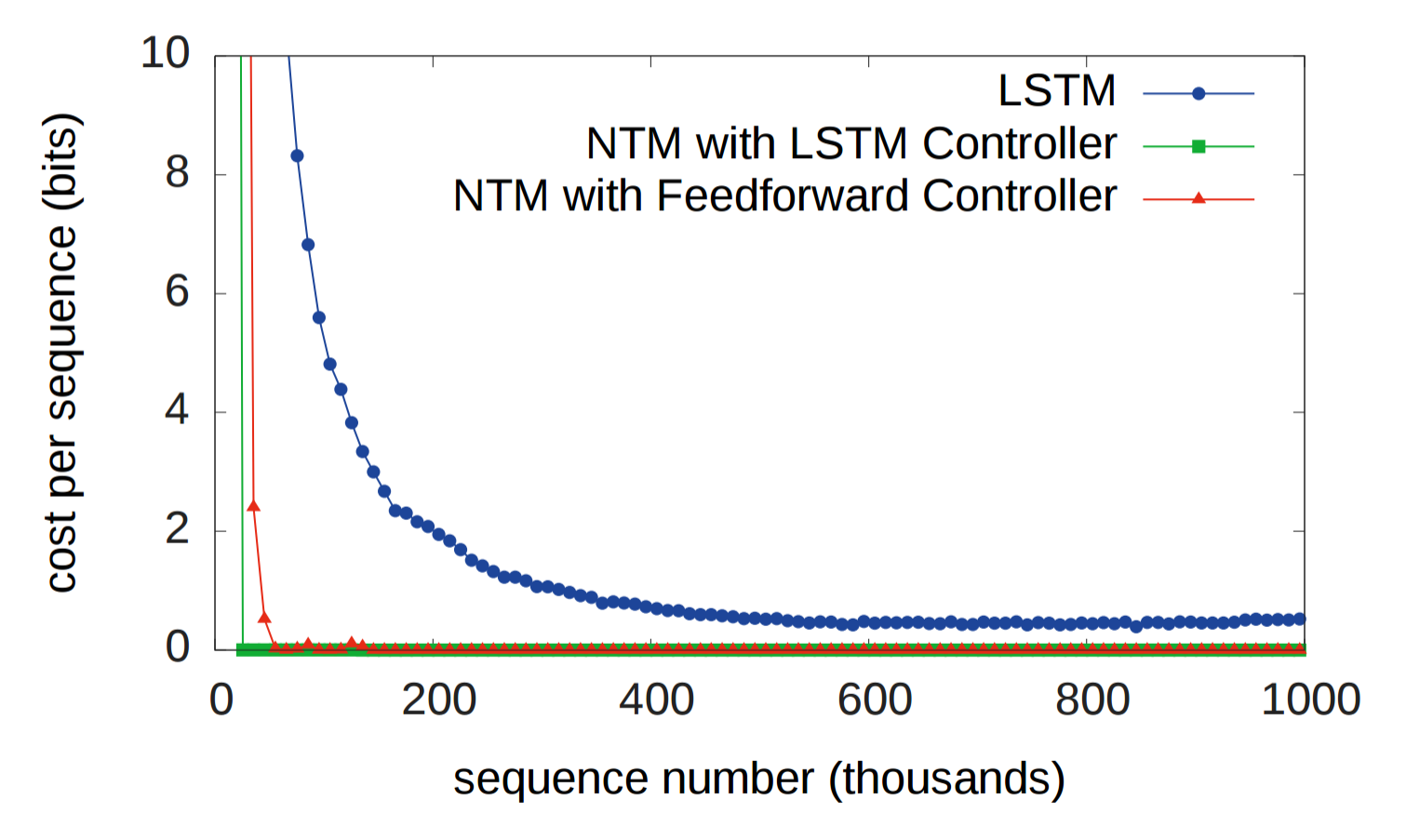
可以看到,NTM的收敛速度、效果都远超单独的LSTM。
接着作者测试了模型的泛化能力:当遇见训练过程中未见过的,更长的序列时,模型不进行任何调整能否正常复制。训练时的序列长度为1到20之间的随机值。
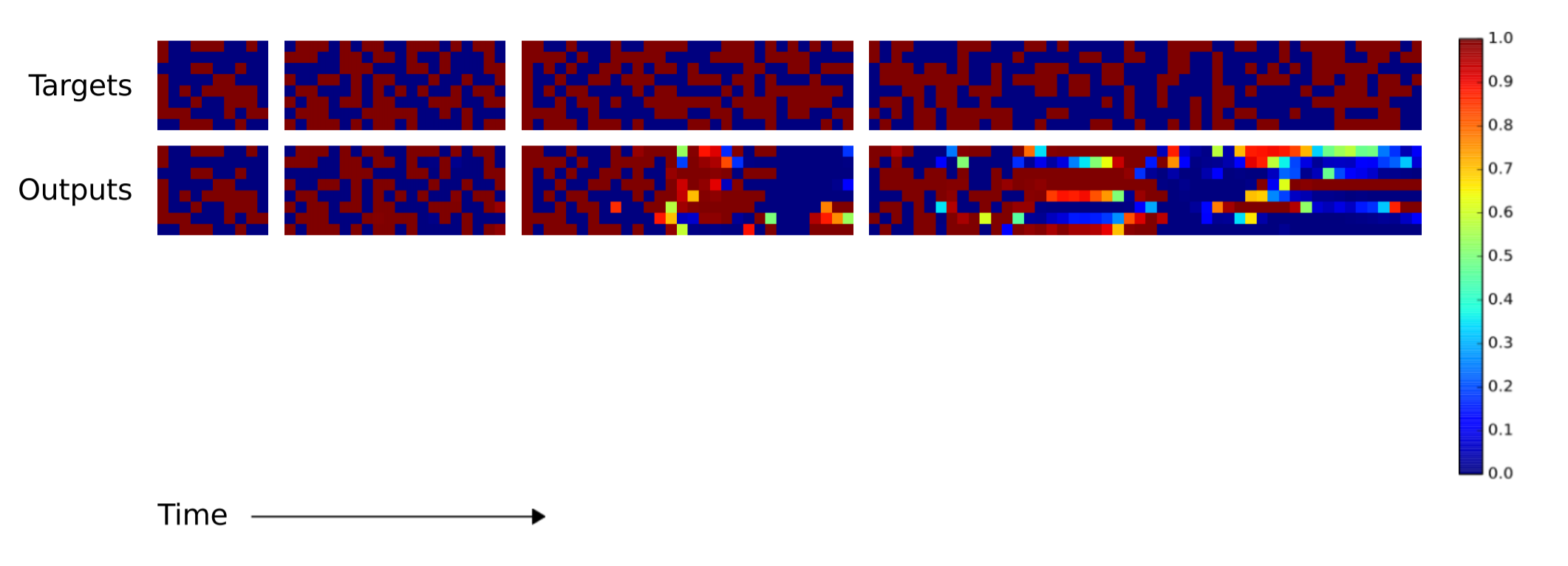

当序列长度少于20时,LSTM与NTM都完成了任务。序列长度继续增加时,相比NTM,LSTM长期记忆信息的能力就明显下降,出现了大量的错误。

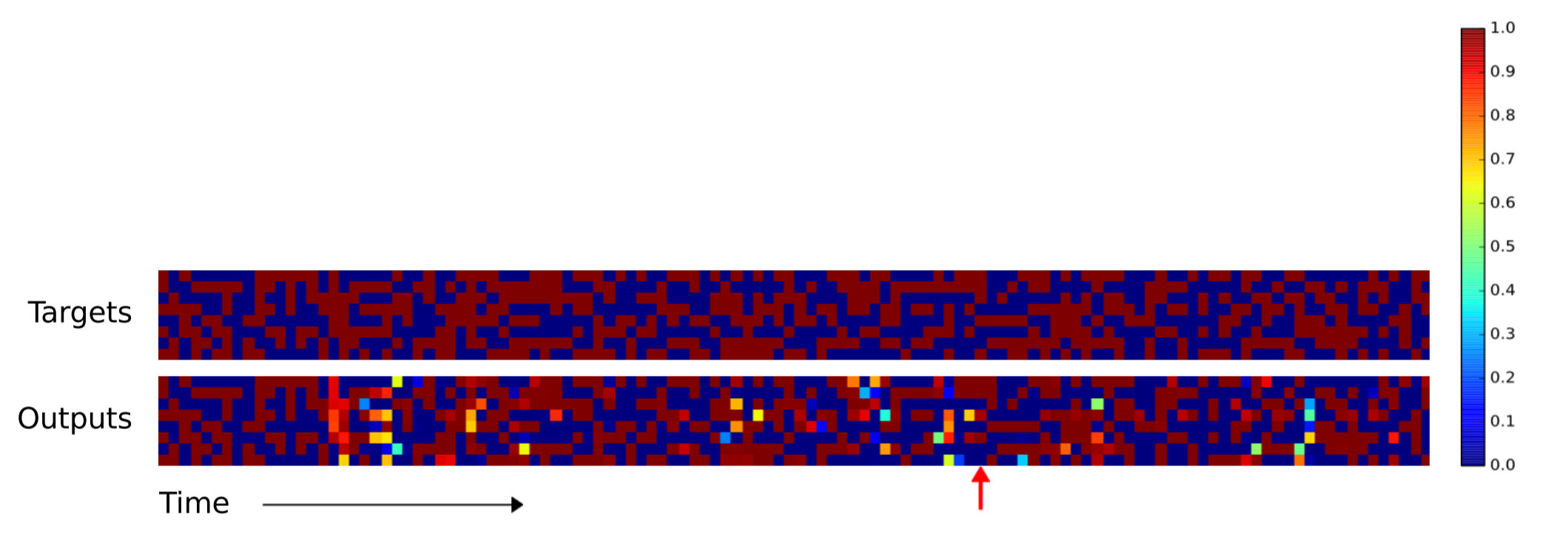
当序列长度增加到120时,LSTM几乎完全无法完成任何复制。NTM在红箭头处之前保持了不错的准确率。然而红箭头处的向量被错误的复制了两遍,导致后面的向量都落后源数据一个时间单位。但除去这个错误,复制误差仍然很低。
接下来,作者分析了算法执行过程中的访存行为。
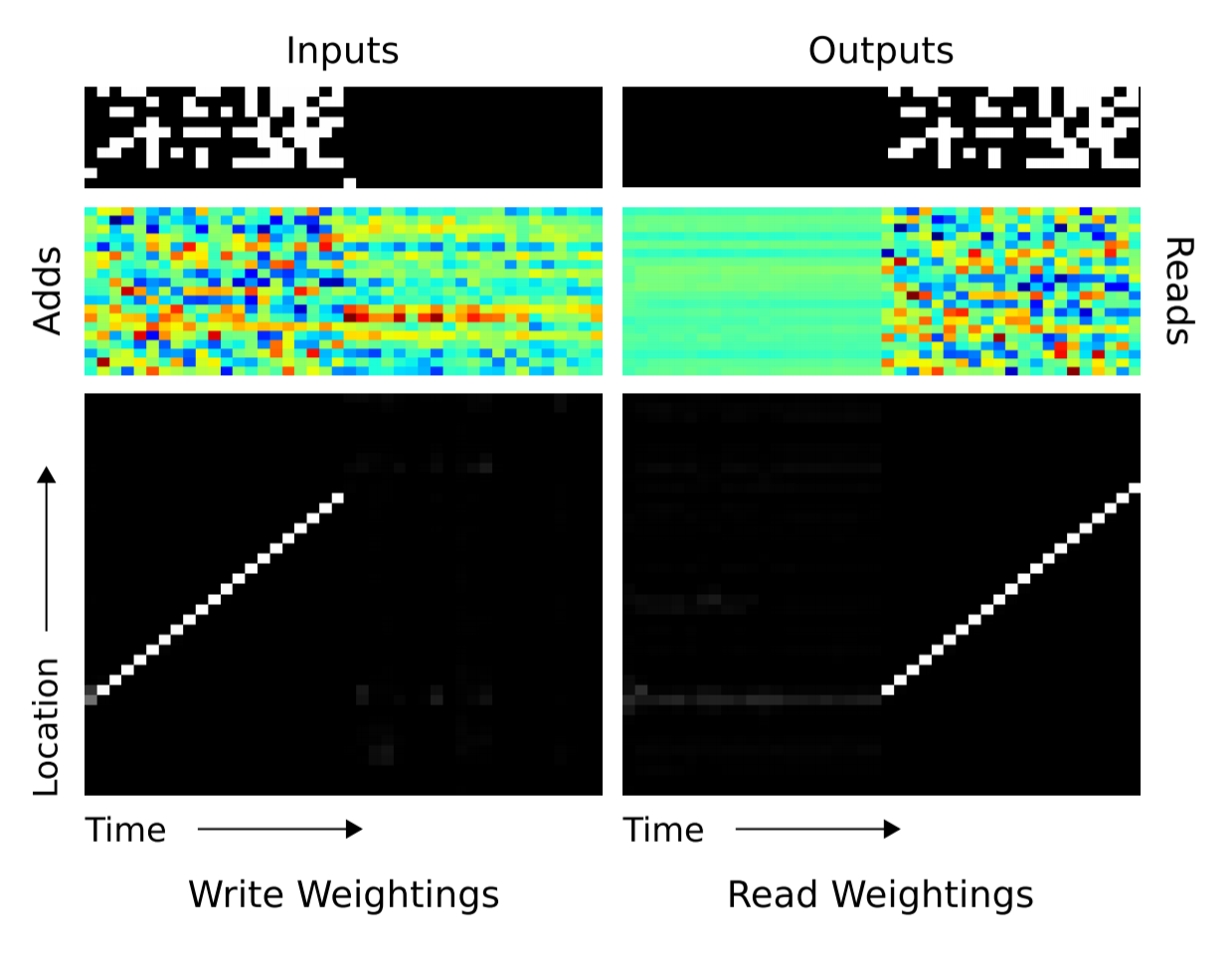
最上方分别是不同时刻输入与输出的向量,中间是每个时刻的$\bm{a}_t,\bm{r}_t$,下方是读写头的位置。
可以看到,NTM逐个地将序列中的向量写入到连续的内存位置,然后在输出阶段逐个读出来。可以说,NTM在这个任务中学会了如何创建数组与遍历数组。
这个结果不仅从功能上验证了NTM有能力模拟复制算法的执行,还从结构上验证了基于内容寻址(读磁头在输出开始时跳到这一段序列的开始)和基于位置寻址(读写头随着时间推移逐步向后移动)的机制。
重复复制
重复复制任务指的是将输入的某个序列复制固定次数,并且在末尾添加终止符。输入为一个序列,和紧接的复制次数,复制次数在1到10之间随机取值并且做了归一化到零均值、单位方差。
作者对性能进行了测试,仍然是NTM取胜:
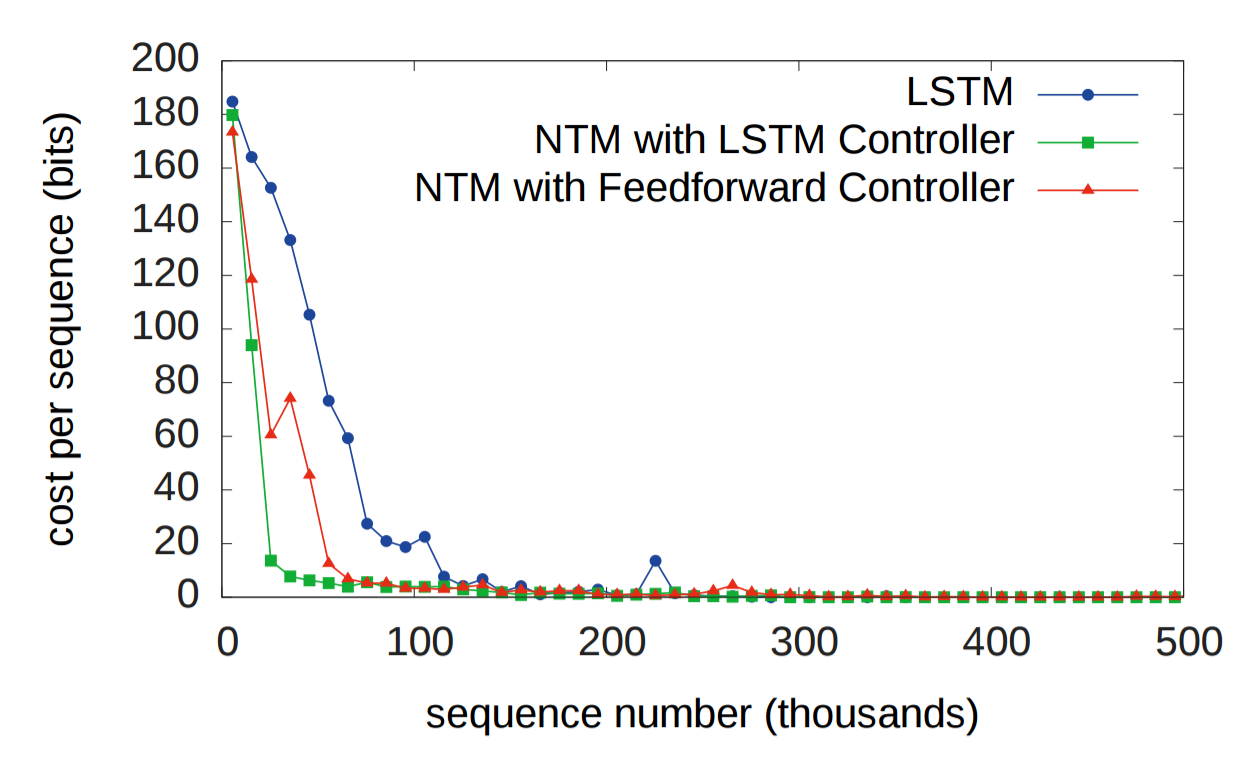
对于数据范围处于训练范围内的情况,LSTM与NTM都能完美解决。因此我们仍然比较泛化能力,这里的泛化能力体现在两个方面:
- 超出训练过程中的序列长度
- 超出训练过程中的重复次数
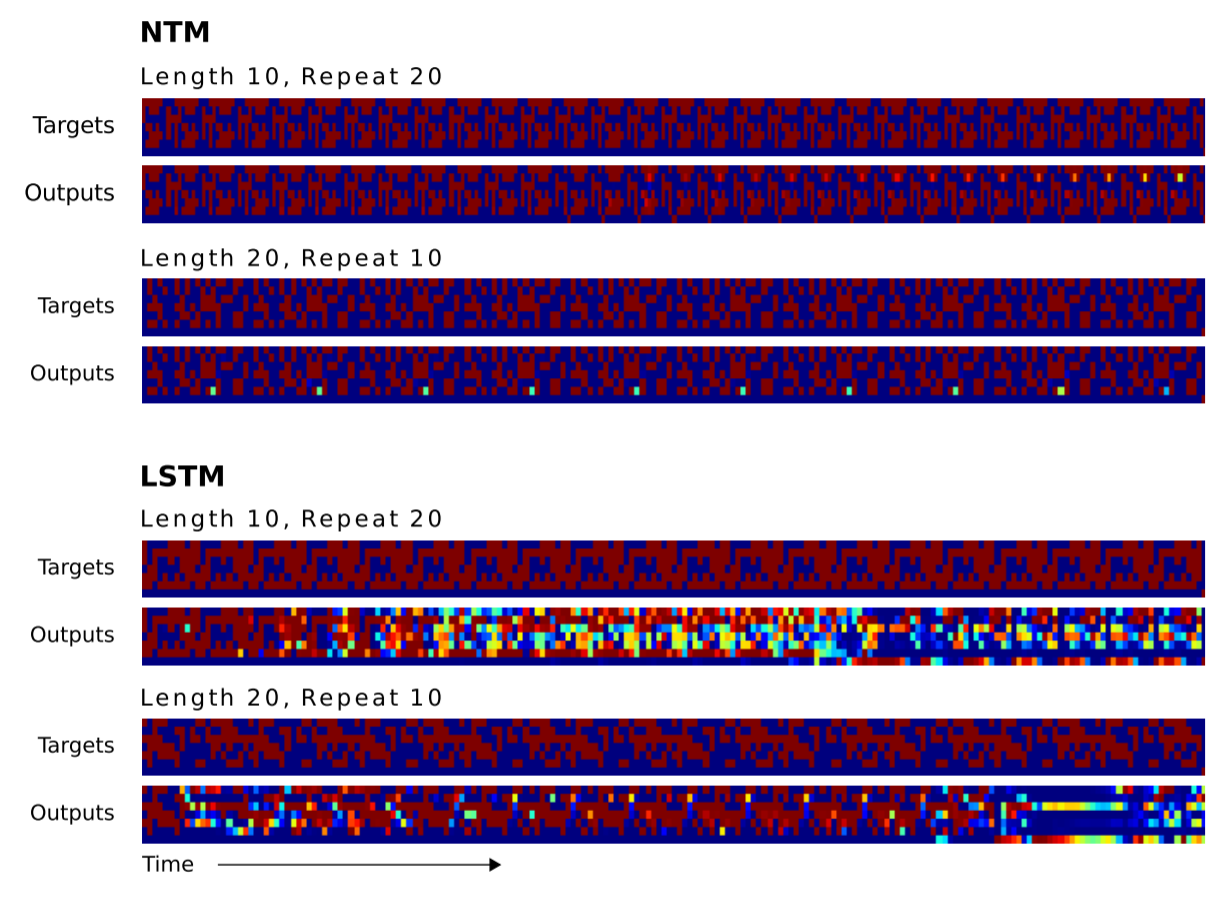
当复制次数超过训练时的最大值10时,NTM仍然能够较好地进行复制。唯一的缺点是还无法理解终止符号,导致复制11次之后的每一次复制都产生了一个终止符。
LSTM则在两种泛化条件下都几乎无法完成任务。
参考文献

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.