• 结构
  • 部件
    • 内存
    • 控制器
• 工作原理
  • 接口向量
  • 读写过程
    • 读
    • 写
  • 寻址机制
    • 基于内容寻址
    • 动态内存分配
      • 读操作——usage衰减
      • 写操作——usage增加
      • 释放过程
      • 写操作权重
    • 时序内存链接
      • 稀疏链接矩阵
    • 读操作权重
• 参考文献

\[\newcommand{\bm}[1]{\boldsymbol{#1}}\]

可微分神经计算机(DNC)可以说是神经图灵机(NTM)的精神续作，并且造了个大新闻，上了Nature¹。不得不说DeepMind出品，必属精品。

结构

论文中给出了如下图示：

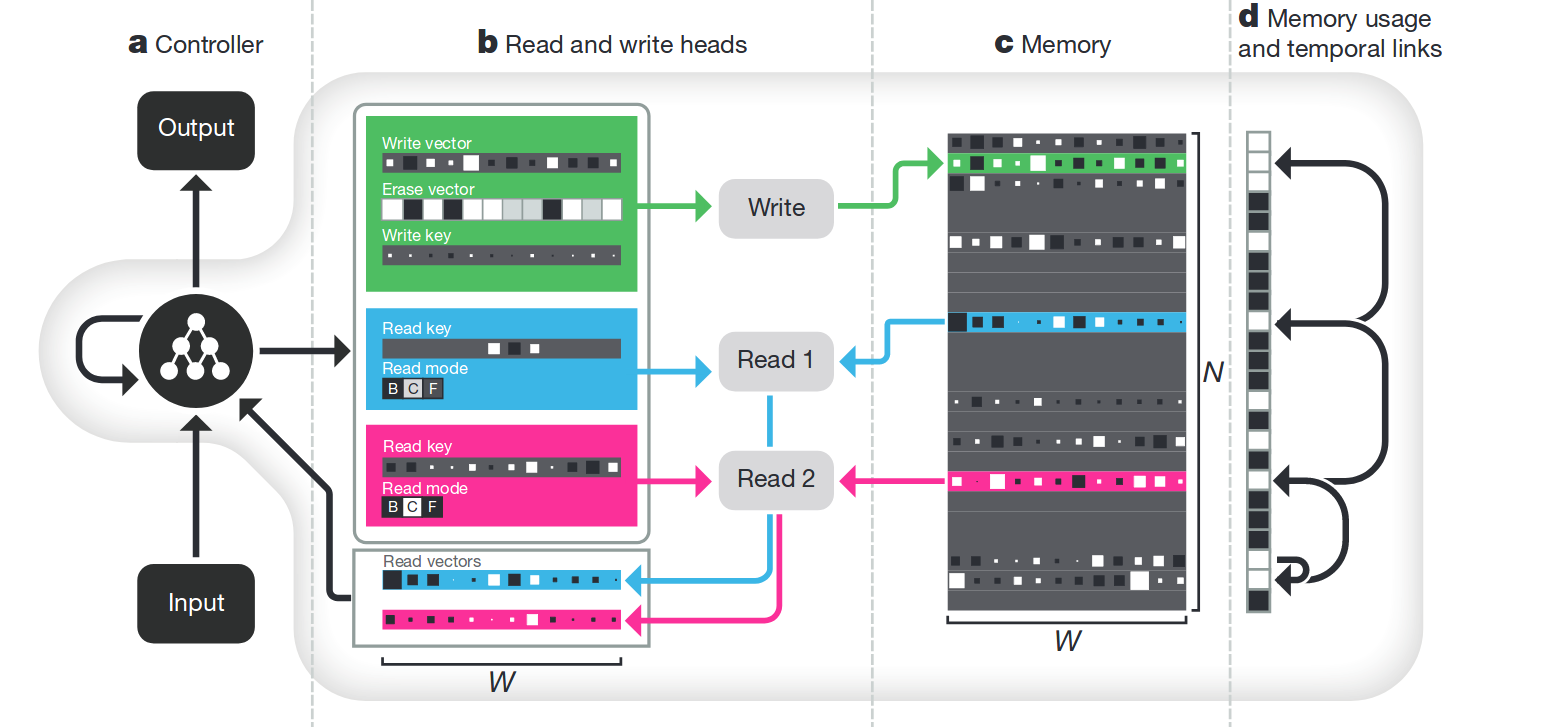
总体来说仍然延续了NTM的那一套设计理念：通过显式的对Memory操作来模拟图灵机的工作。下面将逐个部件地进行分析，同时与NTM进行比较。

部件

内存

跟NTM类似，组织成一个\(N\times W\)的矩阵，共\(N\)个条目，每个条目是长为\(W\)的一个向量。

控制器

相比NTM，这篇文章还算是把控制器结构说清楚了。文中使用了一个LSTM作为控制器。

LSTM每一时刻的输入由上一个时刻中，$R$个读磁头读出的数据\(\bm{r}_{t-1}^1,\dots,\bm{r}_{t-1}^R\in\mathbb{R}^W\)，和这一时刻新的输入\(\bm{x}_t\in\mathbb{R}^X\)连接而成。

\[\bm{\chi}_t=[\bm{x}_t;\bm{r}_{t-1}^1;\dots;\bm{r}_{t-1}^R]\]

假设LSTM有\(L\)个cell，那么第\(l\)个cell的各参数如下

\[\begin{align} \bm{i}^l_t&=\sigma(W_{\bm{i}}^l[\bm{\chi}_t;\bm{h}_{t-1}^l;\bm{h}_{t}^{l-1}]+\bm{b_i}^l)\\ \bm{f}_t^l&=\sigma(W_{\bm{f}}^l[\bm{\chi}_t;\bm{h}_{t-1}^l;\bm{h}_{t}^{l-1}]+\bm{b_f}^l)\\ \bm{s}_t^l&=\bm{f}_t^l\bm{s}_{t-1}^l+\bm{i}_t^l\tanh(W_{\bm{s}}^l[\bm{\chi}_t;\bm{h}_{t-1}^l;\bm{h}_t^{l-1}]+\bm{b_s}^l)\\ \bm{o}_t^l&=\sigma(W_{\bm{o}}^l[\bm{\chi}_t;\bm{h}_{t-1}^l;\bm{h}_{t}^{l-1}]+\bm{b_o}^l)\\ \bm{h}_t^l&=\bm{o}_t^l\tanh(\bm{s}_t^l) \end{align}\]

我们不关心LSTM的输出\(\bm{o}_t^l\)，而只使用其隐藏层的参数\(\bm{h}_t^l\)。

每个时刻，控制器根据隐藏层参数输出两个向量：输出向量\(\bm{\upsilon}_t\)，接口向量(interface vector)\(\bm{\xi}_t\)

\[\begin{align} \bm{\upsilon}_t&=W_{\bm{\upsilon}}[\bm{h}_{t}^{1};\dots;\bm{h}_{t}^{L}]\\ \bm{\xi}_t&=W_{\bm{\xi}}[\bm{h}_{t}^{1};\dots;\bm{h}_{t}^{L}] \end{align}\]

输出向量会直接参与这一时刻输出\(\bm{y}_t\)的生成过程

\[\bm{y}_t=\bm{\upsilon}_t+W_r[\bm{r}_t^1;\dots;\bm{r}_t^R]\]

而如何进行读写（与内存的交互），就全部由接口向量控制，因此接口向量中有大量的参数。

工作原理

接口向量

接口向量\(\bm{\xi}_t\in\mathbb{R}^{(W\times R)+3W+5R+3}\)包含了接下来内存交互中所会用到的参数

\[\bm{\xi}_t=\left[\bm{k}_t^{r,1};\dots;\bm{k}_t^{r,R};\hat{\beta}_t^{r,1};\dots;\hat{\beta}_t^{r,R};\bm{k}_t^w;\hat{\beta}_t^w;\bm{\hat{e}}_t;\bm{v}_t;\hat{f}_t^1;\dots;\hat{f}_t^R;\hat{g}_t^a,\hat{g}_t^w;\bm{\hat{\pi}}_t^1;\dots;\bm{\hat{\pi}}_t^R\right]\]

• \(R\)个read keys：\(\{\bm{k}_t^{r,i}\in\mathbb{R}^W;1\leq i\leq R\}\)（NTM中读磁头的key vector）
• \(R\)个read stength：\(\{\beta_t^{r,i}=\text{oneplus}(\hat{\beta}_t^{r,i})\in[1,\infty);1\leq i\leq R\}\)（NTM中读磁头的key strength）
• write key：\(\bm{k}_t^w\in\mathbb{R}^W\)（NTM中写磁头的key vector）
• write stength：\(\{\beta_t^w=\text{oneplus}(\hat{\beta}_t^w)\in[1,\infty)\}\)（NTM中写磁头的key strength）
• 擦除向量：\(\bm{e}_t=\sigma(\bm{\hat{e}}_t)\in[0,1]^W\)（同NTM）
• 写入向量：\(\bm{v}_t\in\mathbb{R}^W\)（NTM中的加数向量）
• \(R\)个释放门：\(\{f_t^i=\sigma(\hat{f}_t^i)\in[0,1];1\leq i\leq R\}\)
• 分配门：\(g_t^a=\sigma(\hat{g}_t^a)\in[0,1]\)
• 写入门：\(g_t^w=\sigma(\hat{g}_t^w)\in[0,1]\)
• \(R\)个读模式：\(\{\bm{\pi}_t^i=\text{softmax}(\bm{\hat{\pi}}_t^i)\in\mathcal{S}_3;1\leq i\leq R\}\)

其中

\[\begin{align} \text{oneplus}(x)&=1+\log(1+e^x)\\ \mathcal{S}_N&=\left\{\bm{\alpha}\in\mathbb{R}^N:\bm{\alpha}_i\in[0,1],\sum_{i=1}^N\bm{\alpha}_i=1\right\} \end{align}\]

与NTM相较，首先规定了只有一个写磁头，读磁头可以任意多，并且增加了一些“门”。读也有了几个模式。

另外，这里的一些参数范围通过oneplus，sigmoid等函数进行了显式地限制。

读写过程

与NTM相同，每一个磁头的一次读或写都是整个内存各条目的加权和。然而，这里的权值之和并不像NTM总为1，而是可以小于1。这意味着DNC多了一个对内存“什么都不干”的选择。

\[\Delta_N=\left\{\bm{\alpha}\in\mathbb{R}^N:\bm{\alpha}_i\in[0,1],\sum_{i=1}^N\bm{\alpha}_i\leq 1\right\}\]

读

\(R\)个读磁头各有一个读权重向量\(\left\{\bm{w}_t^{r,1},\dots,\bm{w}_t^{r,R}\in\Delta_N\right\}\)，这个权重向量由寻址机制生成（使用了接口向量中的各个参数）。最终读出的\(R\)个向量定义为

\[\bm{r}_t^i=M_t^\top\bm{w}_t^{r,i}\]

写

跟读操作相同，寻址机制会生成唯一一个写磁头的写权重向量\(\bm{w}_t^w\in\Delta_N\)之后，之后跟NTM一样的擦除和覆写过程就是一脉相承了。

\[M_t=M_{t-1}\circ(E-\bm{w}_t^w\bm{e}_t^\top)+\bm{w}_t^w\bm{v}_t^\top\]

这里的\(\circ\)指的是逐元素乘积，\(E\)是全1的\(N\times W\)矩阵。

寻址机制

如果说前面的读写基本继承了NTM的设计，那么寻址机制这一块算是大幅度的改进了。总的来说，寻址机制分为几个部分：基于内容的寻址、动态内存分配、时序内存链接。

基于内容寻址

这里跟NTM相同，根据key与内存中各条目的相似性度量\(\mathcal{D}(\cdot,\cdot)\)来决定对各个位置操作的权重，然后softmax。

\[\mathcal{C}(M,\bm{k},\beta)[i]=\frac{\exp\{\mathcal{D}(\bm{k},M[i,\cdot])\beta\}}{\sum_j\exp\{\mathcal{D}(\bm{k},M[j,\cdot])\beta\}}\]

相似性度量仍然用的是余弦相似度。

\[\mathcal{D}(\bm{u},\bm{v})=\frac{\bm{u}\cdot \bm{v}}{|\bm{u}||\bm{v}|}\]

动态内存分配

由于DNC的内存条目数量是有限的，模拟的算法如果需要大量写入数据的话会遇到内存不足的情形。DNC并没有额外的存储缓存机制，因此只能动态地回收内存。文中所述的是将空闲列表这种内存分配方案转化成了可微分形式应用到DNC中。

具体来说，每个内存位置有一个记录使用情况的数usage，数值越大表示该位置的数据使用越频繁，越重要，这里的内存也越不应该被释放。这些位置的使用情况构成一个向量\(\bm{u}_t\in[0,1]^N\)，一开始\(\bm{u}_0=\bm{0}\)。

大致的逻辑是，每一次写操作会使得该位置的usage增加，之后每次读操作都会使值逐渐衰减。优先释放usage较小的内存位置。

读操作——usage衰减

这里引入新的机制：释放门。不同内存位置的释放门\(f_t^i\)决定了该处的内存每次被读时，usage衰减程度的大小。内存保持程度向量\(\bm{\psi}_t\in[0,1]^N\)表示经过释放门衰减之后，各位置usage剩余的多少。将所有\(R\)个读磁头的结果乘积作为\(\bm{\psi}_t\)。

\[\bm{\psi}_t=\prod_{i=1}^R\left(\bm{1}-f_t^i\bm{w}_{t-1}^{r,i}\right)\]

一次大强度的读和较大的释放门大小会使得该位置的保持向量跌到接近0的位置。

写操作——usage增加

每次写操作会增加该处的usage，这里的公式文中并没有过多的解释，以下是我的解读。

\[\begin{split} \bm{u}'_t&=\bm{u}_{t-1}+\bm{w}^w_{t-1}-\bm{u}_{t-1}\circ\bm{w}^w_{t-1}\\ &={\color{red}(\bm{1}-\bm{w}^w_{t-1})\circ\bm{u}_{t-1}+\bm{w}^w_{t-1}\circ\bm{1}} \end{split}\]

为了看得更清楚，我将论文中的式子作了进一步变换，如红色式子所示。可以看到\(\bm{u}'_t\)实际上是在\(t-1\)时刻的usage与1之间取了一个值。当写的权重越大，新的值就越接近1；即使写的权重很小，新的值也会略微增大。这就保证了

• 写操作总使得usage增加
• 较“强”的写操作会使得usage直接到达1

最终的usage是读写两个操作效果的乘积。

\[\bm{u}_t=\bm{u}'_t\circ \bm{\psi}_t\]

释放过程

有了每个位置的usage之后，我们就可以对其进行升序排序。得到其排序后索引顺序的列表为\(\phi_t\in\mathbb{Z}^N\)。亦即\(\phi_t[1]\)对应的位置usage最小，最可能被释放。

直觉上我们应当直接用\(\bm{1}-\bm{u}_t\)来评估不同位置被释放的可能性的大小，然而这里文中做了一个奇怪的变换

\[\bm{a}_t[\phi_t[j]]=(1-\bm{u}_t[\phi_t[j]])\prod_{i=1}^{j-1}\bm{u}_t[\phi_t[i]]\]

（2019.12.25补充）最近发现，这个变换的目的比较隐晦。我们需要用另一个视角看\(\bm{a}_t\)这个向量。

直觉上，我们希望这是一个衡量概率的向量，那么就需要归一化，也就是和为1。而\(\bm{a}_t[\phi_t[j]]\)其实是一个藏得很深的差分项。 \(\bm{a}_t[\phi_t[j]]=(1-\bm{u}_t[\phi_t[j]])\prod_{i=1}^{j-1}\bm{u}_t[\phi_t[i]]=\prod_{i=1}^{j-1}\bm{u}_t[\phi_t[i]]-\prod_{i=1}^{j}\bm{u}_t[\phi_t[i]]\) 因此对所有的\(\bm{a}_t[\phi_t[j]]\)求和，就会发现。 \(\begin{split} \sum_{i=1}^N\bm{a}_t[\phi_t[i]]&=\sum_{i=1}^N\left(\prod_{j=1}^{i-1}\bm{u}_t[\phi_t[j]]-\prod_{j=1}^{i}\bm{u}_t[\phi_t[j]]\right)\qquad (\prod_{j=1}^{0}\bm{u}_t[\phi_t[j]]=1)\\ &=1-\prod_{i=1}^{N}\bm{u}_t[\phi_t[i]] \end{split}\) 这个结果会非常接近1，也就是起到了归一化的作用。

写操作权重

写磁头经过按内容寻址之后，已经生成了一个初步的权重

\[\bm{c}_t^w=\mathcal{C}(M_{t-1},\bm{k}_t^w,\beta_t^w)\]

结合前面的内存分配的权重\(\bm{a}_t\)，我们可以通过分配门\(g_t^a\)，用两者的加权和来平衡两个寻址机制的结果。最后，写入门\(g_t^w\)决定了这次写操作的强度。

\[\bm{w}_t^w=g_t^w\left[g_t^a \bm{a}_t+(1-g_t^a)\bm{c}_t^w\right],g_t^a\in[0,1]\]

与NTM相比，这里将写入操作看成了两种模式的结合

• 要么写在跟write key相似的地方
• 要么写在空闲或者内容陈旧失效、需要回收的内存位置

而摒弃了偏移的机制，这似乎使得访存不再考虑内存中内容的顺序性、规律性。这对于数组等数据结构是十分不友好的。

时序内存链接

抛弃了偏移机制后，该计算模型对于内存中的序列形式的数据结构就很难处理了。因此，DNC加入了一个时序链接矩阵，显式地存储不同内存位置之间的顺序关系。

时序链接矩阵\(L_t\in[0,1]^{N\times N}\)中的元素\(L_t[i,j]\)的含义是：写入位置j之后，下一个写入位置i的可能性（或者程度之类的）。

为了计算这个矩阵的元素，作者首先计算了在\(t\)时刻，第\(i\)个内存位置是最晚被写入的概率。组成一个向量\(\bm{p}_t\in\Delta_N\)。

\[\begin{split} \bm{p}_0&=\bm{0}\\ \bm{p}_t&={\color{red}{\left(1-\sum_i\bm{w}_t^w[i]\right)\bm{p}_{t-1}}}+{\color{blue}\bm{w}_t^w} \end{split}\]

该式的含义是，如果在\(t\)时刻时，内存位置\(i\)是之前（含\(t\)时刻）所有发生的写操作中最后一次写的位置。那么只有两种可能：

• \(t\)时刻没有发生任何写，这意味着在\(t-1\)时刻之前内存位置\(i\)就已经是最后一次写入的位置
• \(t\)时刻对内存位置\(i\)进行了写操作

两种情况分别对应红色和蓝色的项。

在得到了\(\bm{p}\)之后，就可以比较方便的推出\(L_t\)中的元素。

\[\begin{split} L_0[i,j]&=0\qquad\forall i,j\\ L_t[i,i]&=0\qquad \forall i\\ L_t[i,j]&=(1-\bm{w}^w_t[i]-\bm{w}^w_t[j])L_{t-1}[i,j]+\bm{w}^w_t[i]\bm{p}_{t-1}[j] \end{split}\]

该式的含义是，如果\(t\)时刻时，\(i\)中的内容在\(j\)中内容写入之后才被写入，有以下两种情况

• \(t\)时刻没有对内存位置\(i,j\)写入，那么写入的顺序跟\(t-1\)时刻一致
• \(t\)时刻对内存位置\(i\)进行了写操作，那么之前最后写入的位置必须要是\(j\)

这样我们就用类似链表的形式得到了内存中条目的写入顺序关系。

时序链接矩阵可以指导我们按什么顺序读取内存中的信息。如果我们需要顺着写入的顺序读取，那么就应该找到上一时刻读取的内容对应的下一个内容，新的读权重设为顺序读权重\(\bm{f}_t^i\in\Delta_N\)。那么自然有

\[\bm{f}_t^i=L_t\bm{w}_{t-1}^{r,i}\]

反之，如果我们要逆着写入顺序读取内存中的信息，只要把时序链接矩阵转置一下就可以了。这就得到了逆序读权重\(\bm{b}_t^i\in\Delta_N\)

\[\bm{b}_t^i=L_t^\top\bm{w}_{t-1}^{r,i}\]

以上这套机制的核心是：频繁的内存分配释放使得某个带顺序的数据结构写入内存的位置可能是杂乱无章的。但只要时序内存链接记录了写入时的顺序，那么读取的时候仍然可以按照数据结构本身写入时的顺序（正向或逆向）进行访问。

稀疏链接矩阵

如果直接按照上面的方法求\(L_t\)的话，时间与空间复杂度都将达到\(O(N^2)\)。对于内存较大的情况是无法接受的。文中的实验指出，时序链接矩阵通常是十分稀疏的，因此可以从中设法删去一些信息，降低复杂度，并仍然保持可观的收敛速度。

稀疏化的方法很简单，分以下两步：

1. 在\(L_t\)的计算过程中，将所有的\(\bm{w}^w_t,\bm{p}_{t-1}\)中前\(K\)大分量之外的数置为0，然后做归一化使得前\(K\)大分量的和为1，得到稀疏化后的\(\bm{\hat{w}}^w_t,\bm{\hat{p}}_{t-1}\)。

2. 计算出\(L_t\)后，将\(L_t\)中所有小于\(1/K\)的分量置为0。

复杂度分析

以上过程需要两次\(O(N\log N)\)的排序和两次\(O(K)\)的归一化操作，空间复杂度为\(O(N)\)。然后需要计算下式：

\[\hat{L}_t[i,j]=(1-\bm{\hat{w}}^w_t[i]-\bm{\hat{w}}^w_t[j])\hat{L}_{t-1}[i,j]+\bm{\hat{w}}^w_t[i]\bm{\hat{p}}_{t-1}[j]\]

\(\bm{\hat{w}}^w_t\bm{\hat{p}}_{t-1}^\top\)计算的时间和空间复杂度均为\(O(K^2)\)。\(\hat{L}_{t-1}\)中所有非0元素都\(\geq1/K\)，每行每列的和又至多为1，因而非0元素不超过\(NK\)个，故式子前部的计算时间复杂度为\(O(NK)\)。

接下来顺序读权重和逆序读权重的计算时间复杂度都为\(O(NK)\)，空间复杂度为\(O(N)\)

\[\begin{split} \bm{f}_t^i&=\hat{L}_t\bm{w}_{t-1}^{r,i}\\ \bm{b}_t^i&=\hat{L}_t^\top\bm{w}_{t-1}^{r,i} \end{split}\]

由于\(K\)通常很小（文中\(K=8\)），总的时间复杂度为\(O(N\log N)\)，空间复杂度为\(O(N)\)。

读操作权重

该时刻的写操作结束后，首先根据key与内存中各条目的相似性度量\(\mathcal{D}(\cdot,\cdot)\)来决定对各个位置操作的权重，然后softmax。

\[\bm{c}_t^{r,i}=\mathcal{C}(M_{t},\bm{k}_t^{r,i},\beta_t^{r,i})\]

接下来有三种读模式可选择

• 倒序读：使用\(\bm{b}_t^i\)
• 根据相似度：使用\(\bm{c}_t^{r,i}\)
• 顺序读：使用\(\bm{f}_t^i\)

实际的读结果是根据读模式向量\(\bm{\pi}_t\)加权决定的。

\[\bm{w}_t^{r,i}=\bm{\pi}_t^i[1]\bm{b}_t^i+\bm{\pi}_t^i[2]\bm{c}_t^{r,i}+\bm{\pi}_t^i[3]\bm{f}_t^i\]

参考文献

---

• Previous
  神经图灵机
• Next
  稀疏DNC（一）

---