这个改进模型来自ICLR2019的一篇文章1。第二作者是LSTM的作者之一 Juergen Schmidhuber,一作可能是他的学生。文章思路比较清晰, 有一些值得学习的地方。
改进
文章的题目已经表明了主要内容,总共分三个方向对DNC进行改进。
掩码后基于内容寻址
这个改进是针对基于内容寻址的一个缺陷:key vector是定长的,并且与内存里的条目等长。
假设我们有这样一种需求:只知道key的若干位,要去检索内存中这些位最匹配的内存条目。但在相似度计算时,key中未知的那些位的数据虽然没有意义,但仍然会参与相似度的计算,导致不可预知的结果。并且当已知的位数较少时,其它大多数未知位很有可能都无法匹配,导致生成的相似度权重趋于平坦。
基于这个问题,作者考虑显式地学习内存中究竟哪些位置的信息是有用的,并且在进行相似度计算时摒弃掉无用的部分。
掩码向量\(\bm{m}_t^\ast\in[0,1]^W\),是一个全局的掩码。在计算相似度时,内存中内容与key vector均使用掩码作用之后再计算相似度。
\[C(\bm{M},\bm{k},\beta,\bm{m})[i]=\text{softmax}(D(\bm{k}\odot\bm{m},\bm{M}\odot\bm{1m}^\top)\beta)\]进一步想法
这里考虑的是key vector中部分信息有效的情况,换个角度,memory条目中是否也可能存在这种情况呢?比如某个内存位置存的是一个标志位,其余位都没有作用。
释放内存清零
释放内存清零是一个操作系统内存管理中常见的步骤,即对空闲页写零。不过这里要考虑的问题是,既然不是真正的操作系统,怎么清零,为什么需要清零。
回忆一下,DNC的内存释放过程由若干释放门\(f_t^i\)决定,生成一个内存保持程度向量\(\bm{\psi}_t\in[0,1]^N\)。
\[\bm{\psi}_t=\prod_{i=1}^R\left(\bm{1}-f_t^i\bm{w}_{t-1}^{r,i}\right)\]这个向量会用于衰减usage。
然而,作者意识到完全没有必要这么弯弯绕,先让\(\bm{\psi}_t\)去影响\(\bm{u}_t,\bm{a}_t\),最后到\(\bm{w}_t^w\)。并且这么一层层传过去,很可能衰减的结果就不明显了。
作者重新考虑了\(\bm{\psi}_t\)的本来意义,认为它是用来判断该位置的内容有多大程度应该被保留,数值小的位置就应该被释放。既然如此,那就应该直接根据\(\bm{\psi}_t\)释放内存。但是……DNC里什么是释放呢?
原始DNC的设计中,一层层传过去之后影响的是写的位置权重。换言之,可能被释放的位置应该被写入新内容。但如果一个早就该被释放的位置却一直没有被写入,那么它就还会持续的影响后面的基于内容寻址。因此我们可以考虑直接通过\(\bm{\psi}_t\)来修改内存。
然而如果通过\(\bm{\psi}_t\)直接短路过去操作内存,那么就意味着某些没被写入但需要释放的位置,也该用什么东西填上,来表示这些位置被释放了。
作者机智地注意到:基于内容寻址是根据余弦相似度来的。那么只要把内存中向量置零,余弦相似度就会……没有定义
\[D(\bm{u},\bm{v})=\frac{\bm{u}\cdot\bm{v}}{|\bm{u}||\bm{v}|}\]分母为零不是么。不过一般为了数值稳定,会加个小常数。
\[D(\bm{u},\bm{v})=\frac{\bm{u}\cdot\bm{v}}{|\bm{u}||\bm{v}|+\epsilon}=\cfrac{\cos\langle\bm{u},\bm{v}\rangle}{1+\cfrac{\epsilon}{|\bm{u}||\bm{v}|}}\]这样一来被抹成0的位置的相似度会接近0,下一时刻的基于内容寻址就几乎不会去选这些位置了,从而避免了读取无用的信息。
这个机制的最大好处是解决了内存中过时内容与活跃内容,由于向量内容的相似而导致的混淆问题。
进一步想法
当内存条目只是接近而没有到达零向量时,输出的相似度
\[D(\bm{k},\bm{M}[i,\cdot])\approx\frac{\bm{u}\cdot\bm{v}}{\epsilon}\]反而会很大。
锐化时序链接矩阵
这里的动机其实不那么明显,大致意思是如果写权重不是接近one hot,而是较为平坦时。时序链接矩阵\(\bm{L}_t\)的元素会逐渐衰减,并且引入了此次写权重中的噪声(?)而逐渐变得平坦。
尽管如此,作者还是没有选择直接改\(\bm{L}_t\)(可能是考虑到元素有概率上的意义)。而是对前后向的权重加了一个锐化操作。
\[\bm{f}_t^i=S\left(\bm{L}_t\bm{w}^{r,i}_{t-1},s_t^{f,i}\right)\qquad \bm{b}_t^i=S\left(\bm{L}_t\bm{w}^{r,i}_{t-1},s_t^{b,i}\right)\qquad S(\bm{d},s)_i=\frac{(\bm{d}_i)^s}{\sum_j(\bm{d}_j)^s}\]又是f,跟DNC的释放门符号重了啊……
实际上这里的标量\(s_t^{f,i},s_t^{b,i}\)不是网络直接生成的,而是先生成一个\(\hat{s}_t^{f,i},\hat{s}_t^{b,i}\)再用oneplus限制到\([0,\infty)\)。不过这是细节了。
实验
由于三个技术并不互相依赖,作者将三个技术做了消融实验。用M(asking), D(e-allocation), S(Sharpness enhancement)指代三种技术。实验部分结果如下:
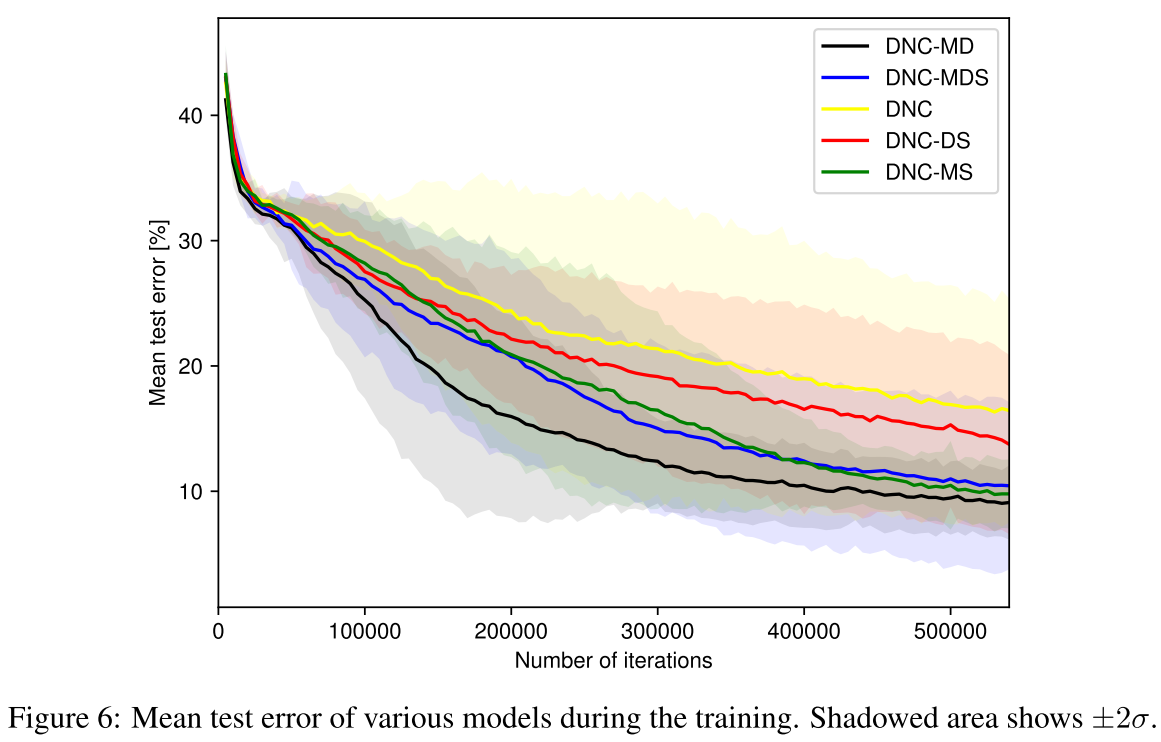
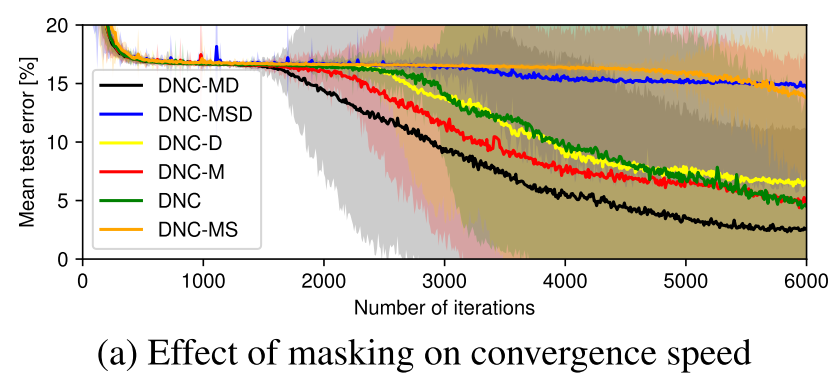
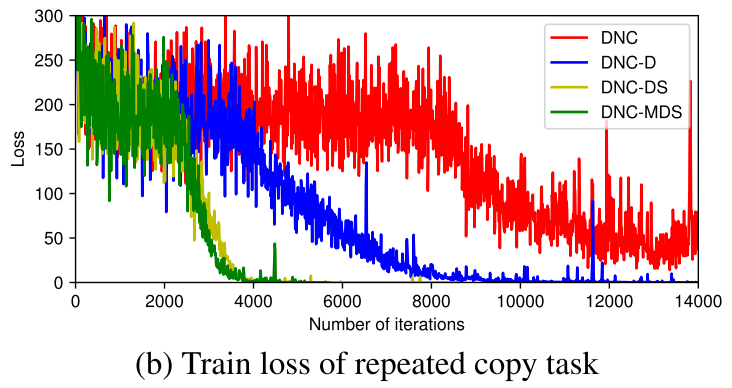
作者发现在associative recall任务与bAbI数据集上都是DNC-MD表现最佳。只有在repeated copy上才是DNC-MSD最佳。甚至在associative recall任务上,带S的版本还远不如原始的DNC。
掩码机制对于associative recall任务大大加速了收敛速度。文中的另一个key-value retrieval明显是量身定做的任务,之前的DNC中没有出现。
新的释放机制对于associative recall影响不大,但显著提高了repeated copy的收敛速度。作者猜测是因为内存中的多个相同数据现在可以分辨新旧了(新机制下会被显式释放)。
锐化机制看起来只有在任务有明显的维护顺序数据结构时才有用,在其他任务上反而拉低性能,可以认定只是个针对特定任务的trick。(甚至连DNC-S的实验都没有……)不过这里可借鉴的经验的是:作者发现了在没有锐化机制时,\(\bm{L}_t\)的确可能会变得平滑而导致两种读模式(正向、逆向)失去意义,从而读操作开始偏爱基于内容寻址的模式(另外两种读模式没有信息来源了)。
参考文献
-
Csordás, R., & Schmidhuber, J. (2019). Improving Differentiable Neural Computers Through Memory Masking, De-allocation, and Link Distribution Sharpness Control. International Conference on Learning Representations. ↩

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.