前言
入坑SNN已半年有余,目前自己的论文阅读量勉强可以达到听懂今年的workshop中大多数讲座,以及对介绍的工作能提出自己的问题。另外实验室的脉冲神经网络框架SpikingJelly也在稳步推进中,可以说研究工作暂时步入了正轨。
这次听讲座的目的很简单:看看大佬们了解什么我不知道的事情,收集并分析信息,帮助决定进一步的研究方向。一般来说,科研中很多思路性的东西往往不会详细在论文里叙述,但容易体现在科研人员的交流过程中。在workshop中很多大佬也的确乐于分享实验室在投(如挂在预印本平台上的)甚至是正在进行实验的文章细节,是绝对的前沿资讯,不可错过。
言归正传,来看看今年各个大佬的研究组都出了些啥进展
会议提要
以下是总结的会议精神![]()
Bohte组
Sander Bohte来自荷兰阿姆斯特丹信息与数学科学中心(Centrum Wiskunde & Informatica, CWI),是研究SNN并且将反向传播算法应用至SNN上的早期研究者,在其攻读博士期间以一作身份在Neurocomputing上发表了经典之作SpikeProp1,迄今仍然有各种改进其技术的文章。之后若干年也笔耕不辍。他们这次拿出来的文章是刚刚中ICONS2020的SRNN2。
首先,Bohte指出LIF神经元对数据的编码方式实际上是$\Sigma$-$\Delta$模数转换器的变体。对于输入编码,在以下两个条件满足时是有效的
-
发放率较低
-
后突触电位(Postsynaptic Potential, PSP)衰减较慢
一个示例如下图:
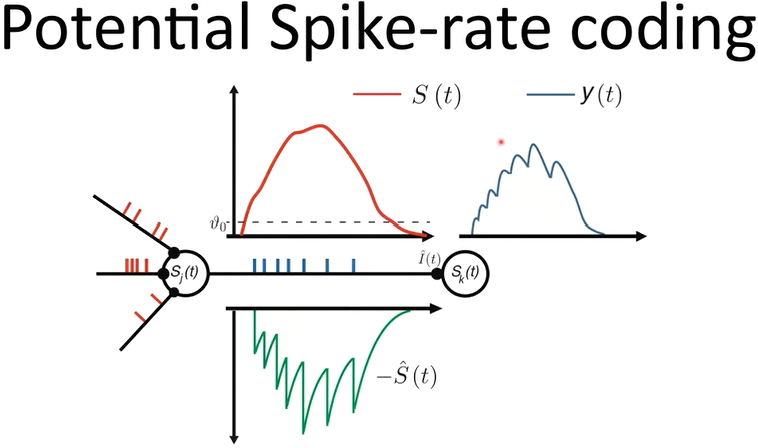
以神经元$S_j$为基准,红色的为前突触输入在LIF神经元上的累计膜电位(即假定神经元不发放时的膜电位)。每一次越过发放阈值$\vartheta_0$时,就会向后突触发放脉冲并引起相应的refractory response(绿色),最终导致$S_k$上的PSP如蓝色曲线所示。
可以看到,PSP的形状一定程度上和输入信号的累计形状是类似的。前者可以视作对后者的一种高度近似。下图中,两个信号的相似程度则更加明显。
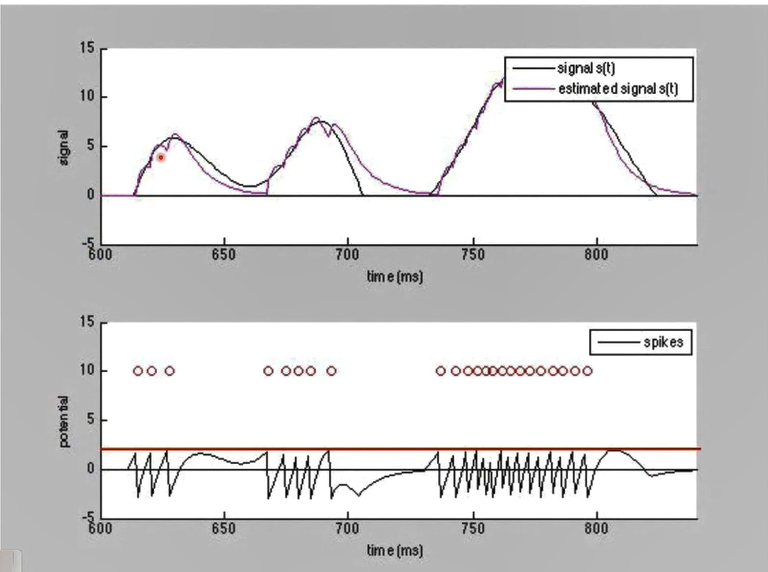
但这种近似的效果往往会受到参数制约,如下图所示,假如神经元的发放阈值进一步降低,对于一般位置的输入拟合将更加精细。但当输入信号很强时,神经元将达到最大发放率而饱和,对于越过该值的信号将无法准确拟合。
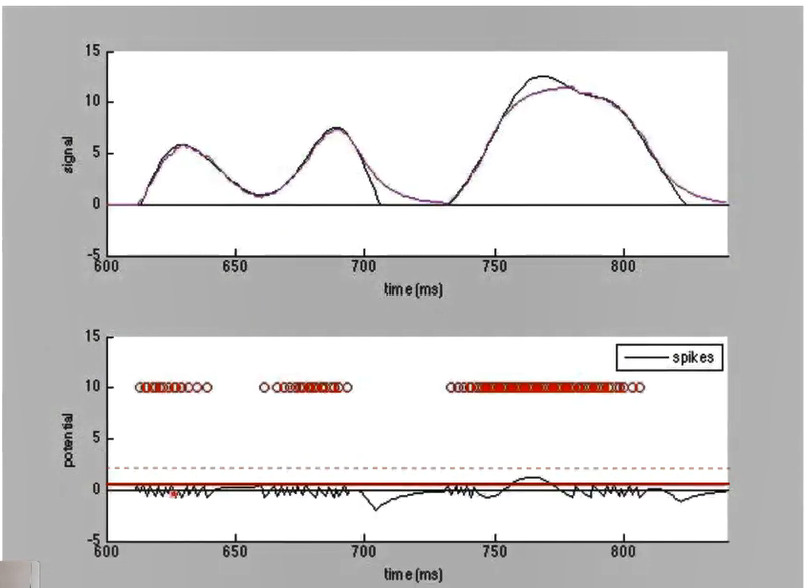
另一方面显然的是,当神经元的发放阈值过高,将捕捉不到任何脉冲信号。
这里我们看到当输入信号一定时,阈值的降低能够提高编码的精细程度。但同时对于极端值(发放率超过饱和值)的编码能力不足。因此阈值的设置应当能够随着发放率的变化适应性的调节。这就是适应性(Adaptive)神经元的由来。
适应性神经元也并非什么新东西,Izhikevich3和AdEx(Adaptive exponential integrate-and-fire)4模型都是本世纪初就提出的适应性神经元模型。这些神经元的通常构建方法通常是给神经元的某个参数增加一个动态方程,这个参数的动态方程和神经元的膜电位方程一样,用微分方程描述。作者文章中的神经元也不例外,将动态方程加在了阈值上。
具体来说,作者希望阈值也随着脉冲的发放而相应的提高,在没有脉冲时指数衰减,与膜电位的行为一致,但使用不同的膜电位参数$\tau$。用$\theta$表示神经元的阈值,$u_t$表示$t$时刻的膜电位,阈下动态方程可以描述如下:
\[\begin{align} \alpha&=\exp(-\mathrm{d}t/\tau_m)\\ \rho&=\exp(-\mathrm{d}t/\tau_{adp})\\ \eta_t&=\rho\eta_{t-1}+(1-\rho)S_{t-1}\\ \theta&=b_0+\beta\eta_t\\ u_t&=\alpha u_{t-1}+(1-\alpha)R_mI_t-S_{t-1}\theta \end{align}\]其中$\tau_m,\tau_{adp}$都是可训练的参数,并且每个神经元不共享这两个参数,对整个网络用替代梯度进行训练。
总的来说,将Adaptive神经元引入并不算特别创新,但是这个方法一定程度上解决了SNN在编解码上面的问题。官方代码实现位于Github。
最后感受一下Sander Bohte对于“Yann LeCun之问”的隔空回应![]()

Wolfgang Maass组
这个组在机器学习理论领域与计算神经科学领域内几乎是无人不知无人不晓了,这次直接带出一篇Nature Communications就问你怕不怕(当然他们组正刊都有很多篇)。好在这篇文章还在审时我们就看过一遍并且讨论过了,因此能比较容易跟上作者的演讲思路。
本文利用资格迹(eligibility trace)解决了单层RNN(当然也包括单层SNN)的在线训练问题,以及提出了一种近似BPTT的在线训练算法e-prop5。
……未完待续
参考文献
-
Bohte, S. M., J. N. Kok and H. La Poutre (2002). “Error-backpropagation in temporally encoded networks of spiking neurons.” Neurocomputing 48: 17-37. ↩
-
Yin, B., F. Corradi and S. M. Bohté (2020). Effective and Efficient Computation with Multiple-timescale Spiking Recurrent Neural Networks. International Conference on Neuromorphic Systems 2020: 1-8. ↩
-
Izhikevich, E. M. (2003). “Simple model of spiking neurons.” IEEE transactions on Neural Networks 14(6): 1569-1572. ↩
-
Brette, R. and W. Gerstner (2005). “Adaptive exponential integrate-and-fire model as an effective description of neuronal activity.” Journal of Neurophysiology 94(5): 3637-3642. ↩
-
Bellec, G., F. Scherr, A. Subramoney, E. Hajek, D. Salaj, R. Legenstein and W. Maass (2020). “A solution to the learning dilemma for recurrent networks of spiking neurons.” Nature Communications 11(1): 3625. ↩

This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license.